Zwei parallele Geraden
4. Zwei echt parallele Geraden, die in der Ebene liegen sollen
Geg.: g: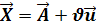 
h: 
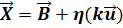
Zwei Geraden können nur dann parallel sein, wenn ihre Richtungsvektoren Vielfache voneinander sind. Um dies auszudrücken, wurde die Schreibweise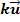 
für den Richtungsvektor der Gerade h gewählt. In Worten:Der Richtungsvektor von h ist das k-fache von g.
Im vorhergehenden Abschnitt wurde erklärt, wie man mit zwei sich schneidenden Geraden eine Ebenengleichung aufstellt. Man verwendet einfach einen der beiden Aufpunkte der Geraden als Aufpunkt der Ebene und nimmt die beiden Richtungsvektoren der Geraden als Richtungsvektoren der Ebene. Aber nicht nur durch zwei sich schneidende Geraden, sondern auch durch zwei echt parallele Geraden ist eine Ebene eindeutig festgelegt. Da jedoch die beiden Richtungsvektoren paralleler Geraden Vielfache voneinander sind, sind sie linear abhängig bzw. kollinear und spannen keine Ebene auf. Man darf also bei parallelen Geraden nicht wie bei sich schneidenden Geraden einfach die beiden Richtungsvektoren der Geraden als Richtungsvektoren der Ebene verwenden! Einen der Richtungsvektoren von g oder h kann man als Richtungsvektor der Ebene benützen, aber nicht den zweiten!
Wie bildet man nun aber den zweiten Richtungsvektor? Betrachte dazu die folgende Skizze!
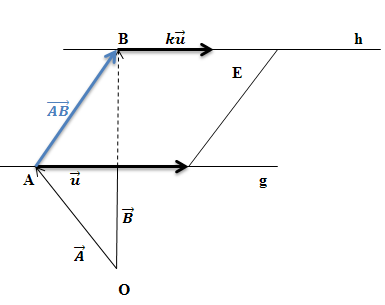
Anmerkung zur Skizze:Die Geraden g und h liegen eigentlich nicht am Rand der Ebene, auch wenn das in der Skizze so aussieht. Sie liegen eigentlich irgendwo innerhalb der Ebene. Eine Ebene hat bekanntlich gar keinen Rand, sie geht unendlich weiter! Diese Art der Darstellung wurde nur ihrer Einfachheit wegen gewählt. Diese Skizze soll nur veranschaulichen, wie man eine Ebenengleichung aufstellen kann, wenn zwei parallele Geraden gegeben sind, die in der Ebene liegen sollen.
Da die beiden Geraden g und h in der Ebene E liegen, liegen auch die Aufpunkte A und B der Geraden in der Ebene. Einen der beiden Punkte machen wir zum Aufpunkt der Ebene, beispielsweise A. (Natürlich hätte man stattdessen auch B als Aufpunkt der Ebene verwenden können.) Den zweiten Aufpunkt dürfen wir bei parallelen Geraden nicht einfach aus unserer Überlegung ausschließen. (Bei sich schneidenden Geraden wird der zweite Aufpunkt beim Aufstellen der Ebenengleichung völlig ignoriert.) Als zweiten Richtungsvektor verwenden wir bei parallelen Geraden den Verbindungsvektor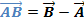 
der beiden Aufpunkte der Geraden. Da der Vektor 
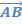zusammen mit einem der beiden Richtungsvektoren der Geraden, z.B. 
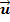die Ebene aufspannt, kan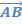n neben 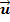als zweiter Richtungsvektor der Ebene verwendet werden. Vergleiche Skizze!
Daher lautet der Ansatz für die Parameterform der Ebene E, die durch die parallelen Geraden g und h festgelegt ist:
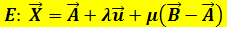
Möchtest du also eine Ebene mit zwei parallelen Geraden aufstellen, kannst du einfach eine Geradengleichung abschreiben und als zweiten Richtungsvektor der Ebene den Verbindungsvektor der beiden Aufpunkte (Ortsvektoren der beiden Aufpunkte voneinander abziehen) dahinter setzen.
Bsp.:Ermittle eine Gleichung der Ebene E, welche die beiden Geraden g und h enthält!
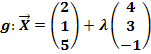
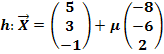
Lösung:
Wir bezeichnen wie bisher den Aufpunkt der Gerade g mit A und den Richtungsvektor von g mit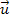 
. Den Aufpunkt der Gerade h nennen wir wieder B. Offensichtlich sind die beiden Richtungsvektoren Vielfache voneinander. Der Richtungsvektor der Gerade h ergibt sich, wenn man den Richtungsvektor 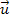der Gerade g mit dem Faktor -2 multipliziert. Daher sind die beiden Geraden entweder echt parallel zueinander oder sie sind identisch. Wären sie jedoch identisch, würden sie keine Ebene festlegen. Eigentlich müsste daher zuerst die Punktprobe gemacht werden, bevor man die Ebenengleichung aufstellt. So könnte man sicherstellen, dass der Aufpunkt der einen Gerade nicht auf der anderen Gerade liegt. Dann sind die beiden Geraden wirklich echt parallel und nicht etwa identisch. Wir übergehen hier allerdings die Punktprobe, da man auch am Endergebnis der Parametergleichung der Ebene erkennen kann, dass wirklich eine Ebene festgelegt ist. Man erkennt dies daran, dass die beiden Richtungsvektoren der Ebene linear unabhängig / nicht kollinear (keine Vielfachen voneinander) sind. Es muss daher nicht unbedingt vorher nachgewiesen werden, dass die Geraden echt parallel sind. Wir stellen sofort die Ebenengleichung auf:
Dazu verwenden wir einen der beiden Aufpunkte der Geraden, beispielsweise den Punkt A als Aufpunkt der Ebene. Den ersten Richtungsvektor der Ebene erhalten wir, indem wir einfach einen Richtungsvektor der Geraden nehmen.
Vorsicht:Du darfst bei parallelen Geraden auf keinen Fall den Richtungsvektor der anderen Gerade als zweiten Richtungsvektor der Ebene verwenden! Da er ein Vielfaches des ersten Richtungsvektors ist, würden diese beiden Vektoren gar keine Ebene aufspannen. Daher dürfen bei parallelen Geraden keinesfalls beide Richtungsvektoren der Geraden als Richtungsvektoren der Ebene verwendet werden.
Den zweiten Richtungsvektor der Ebene erhalten wir, indem wir den Verbindungsvektor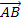 
der beiden Aufpunkte bilden.
Geg.: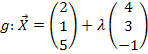 
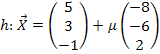
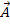
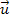
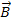
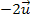
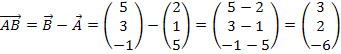
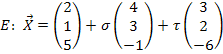
Die Richtungsvektoren der Ebene sind offensichtlich keine Vielfachen voneinander, daher ist eindeutig eine Ebene festgelegt.
Du hast nun gesehen, wie eine Ebene mit zwei sich schneidenden oder mit zwei echt parallelen Geraden aufgestellt werden kann. Da nur bei sich schneidenden Geraden beide Richtungsvektoren der Geraden als Richtungsvektoren der Ebene verwendet werden dürfen, muss du immer, wenn du eine Ebene mit zwei Geraden aufstellen sollst, vorher überlegen, wie die Geraden zueinander liegen, ob sie sich schneiden oder echt parallel sind!
