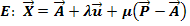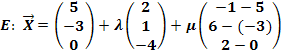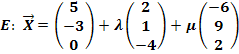Ein Punkt und eine Gerade
2. Ein Punkt P und eine Gerade g, wobei P nicht auf g liegt
Die Gerade und der Punkt sollen in der Ebene E liegen.
Geg.: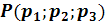 
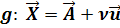
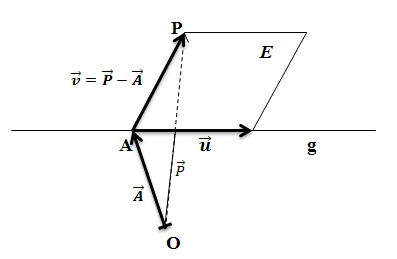
Als Aufpunkt der Ebene kann man entweder den Punkt P oder den Aufpunkt der Gerade g, hier mit A bezeichnet, verwenden. Wir entscheiden uns für den Aufpunkt der Gerade A. Als ersten Richtungsvektor der Ebene können wir den Richtungsvektor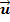 
der Gerade nehmen. Den zweiten Richtungsvektor 
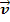der Ebene bildet der Vektor 
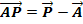, wie man in der Zeichnung erkennen kann. Daher lautet der Ansatz für die Parametergleichung einer Ebene E, wenn ein Punkt P und eine Gerade 
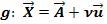gegeben sind, die in der Ebene E liegen:
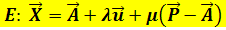
Diese Formel steht nicht in der Formelsammlung! Du musst sie dir eigentlich selbst herleiten, was mit Hilfe der oben gezeigten Skizze jedoch kein Problem darstellen sollte. Präge dir deshalb die Zeichnung gut ein, damit du sie selbst jeder Zeit schnell aufskizzieren kannst!
Bsp.: Ermittle eine Gleichung der Ebene E in Parameterform, die den Punkt P(-1| 6| 2) und die Gerade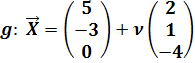 
enthält!
Lösung:
Zuerst überprüfen wir, ob der Punkt P auf der Gerade g liegt. Damit überhaupt eine Ebene durch P und g festgelegt ist, darf P nicht auf g liegen! Den Nachweis dafür, dass P nicht auf g liegt, erbringt man folgendermaßen:
· P für X in g einsetzen
· Jede der drei Zeilen einzeln als Gleichung schreiben
· Jede der drei Gleichungen nach dem Parameter, hier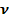 
, auflösen
· Es ergeben sich verschiedene Ergebnisse für den Parameter (Es darf also nicht dreimal das gleiche für herauskommen, denn sonst würde P auf g liegen.)
Manche Lehrer bezeichnen dieses Verfahren auch als „Punktprobe“.
P 
g ? 
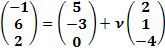
I.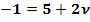 
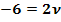
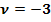
II.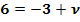 
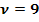
III.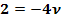 
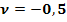
Es haben sich für 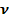drei verschiedene Werte, also ein Widerspruch ergeben, daher liegt der Punkt P nicht auf der Gerade g. P und g legen eindeutig eine Ebene fest. Nun kann die Gleichung der Ebene E ermittelt werden.
Geg.: P(-1| 6| 2)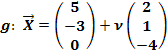 
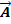
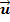
Wir wählen den Aufpunkt der Gerade als Aufpunkt der Ebene. (Man hätte auch den Punkt P als Aufpunkt der Ebene verwenden können. Jeder Punkt, der in der Ebene liegt, kann als Aufpunkt der Ebene benützt werden.) Der eine Richtungsvektor der Ebene ist der Richtungsvektor 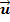der Geraden, der zweite Richtungsvektor ist der Verbindungsvektor 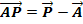. Vergleiche dazu noch einmal die Skizze oben!
