Hesse-Normalenform einer Ebene
Unter der sogenannten Hesse-Normalenform, kurz HNF genannt, versteht man die Normalenform einer Ebene, die den Einheitsnormalenvektor verwendet, der (ausgehend von einem Punkt in der Ebene) weg zeigt vom Ursprung.
Zur Wiederholung:Ein Einheitsvektor hat immer die Länge, also den Betrag 1. Zu jedem Vektor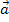 
gibt es einen Einheitsvektor 
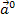, der die selbe Richtung, aber die Länge bzw. den Betrag 1 hat. Man berechnet 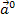mit der Formel: 
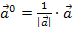bzw. 
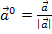
Entsprechend wird der Einheitsnormalenvektor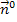 
zum Normalenvektor 
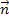gebildet:
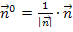bzw.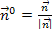 
Woran erkennt man nun aber, ob der Normalenvektor zum Ursprung hin oder vom Ursprung wegschaut?
In der Koordinatenform einer Ebene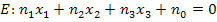 
erkennt man das am Vorzeichen der Konstante 
:
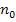Ist das Vorzeichen von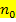 
negativ, dann schaut der Normalenvektor vom Ursprung weg, wie in der Hesse-Normalenform verlangt. Ist aber das Vorzeichen der Konstante positiv, schaut der Normalenvektor für die Hesse-Normalenform in die falsche Richtung. Man muss dann alle Vorzeichen der Koordinatenform umdrehen, wenn man die Hesse-Normalenform bilden will.
Die Hesse-Normalenform einer Ebene verwendet man vor allem bei der Berechnung des Abstands eines Punktes von einer Ebene. Aber auch bei anderen Aufgaben, die z.B. etwas mit Abständen von Ebenen oder windschiefen Geraden zu tun haben, sowie bei der Ermittlung von Winkelhalbierendenebenen ist sie sehr praktisch. Da die mathematisch korrekte Darstellung der Hesse-Normalenform für die meisten Schüler nur verwirrend wäre, soll sie auf dieser website erst später gezeigt werden. Im Folgenden wird an einem Beispiel gezeigt, wie die Hesse-Normalenform gebildet wird.
1. Bsp.:Ermittle die Hesse-Normalenform der Ebene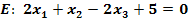 
!
