Zueinander senkrechte (orthogonale) Geraden

Zwei Geraden, die sich unter einem Winkel von 90° schneiden, bezeichnet man als orthogonale Geraden. Orthogonal bedeutet daher nichts anderes als zueinander senkrecht.

Es soll nun überprüft werden, ob die Geraden und orthogonal, also zueinander senkrecht verlaufen.

Versuche nun selbst die beiden Geraden in ein Koordinatensystem zu zeichnen! (Platzbedarf: und )

Zur Erinnerung:Das Steigungsdreieck zeichnest du folgendermaßen:Denke dir die Steigung m als Bruch! Den Nenner gehst du immer nach rechts. Den Zähler gehst du nach oben, wenn m positiv, bzw. nach unten, wenn m negativ ist. Genaueres zum Einzeichnen von Geraden findest du im Kapitel Lineare Funktionen zeichnen.

Die Geraden und sind in der Abbildung 8.52 dargestellt. Sie liegen scheinbar zueinander senkrecht, d.h. es handelt sich vermutlich um orthogonale Geraden.

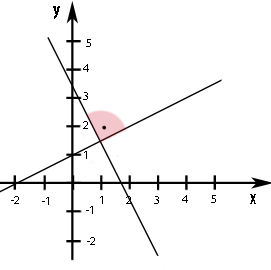
Abb. 8.52 Darstellung der Geraden und

Wie kann man nun überprüfen, ob diese zwei Geraden wirklich zueinander senkrecht sind oder nicht? Man könnte z.B. versuchen ihren Schnittwinkel mit einem Geodreieck abzumessen. Dass dies aber keine wirklich genaue Methode ist, leuchtet sicherlich von selbst ein. Wie könnte man beispielsweise durch bloßes Abmessen einen 89,99° – Winkel von einem 90° – Winkel unterscheiden? Man braucht also eine andere, rein rechnerische Methode, um nachzuweisen, dass zwei Geraden zueinander senkrecht, also orthogonal sind.

Gegeben sind die beiden Geraden und .

In Worten:Zwei Geraden und sind zueinander senkrecht (orthogonal), wenn ihre Steigungen und miteinander multipliziert -1 ergeben.

Auf die Herleitung dieser Formel wird absichtlich verzichtet, da du sie sowieso nicht brauchst und sie außerdem Vorkenntnisse über die Schnittwinkelberechnung mit Hilfe des Tangens verlangt. Die Schnittwinkelberechnung zweier linearer Funktionen ist jedoch erst Stoff der gymnasialen Oberstufe.

Mit dieser Formel können wir jetzt rechnerisch überprüfen, ob die oben dargestellten Geraden und wirklich senkrecht zueinander sind. Die Gerade hat die Steigung . Die Gerade hat die Steigung . Nun bilden wir das Produkt und überprüfen, ob sich das Ergebnis -1 ergibt:

Die beiden Geraden und sind tatsächlich zueinander senkrecht (orthogonal).

Häufig wird auch die umgekehrte Aufgabe gestellt, dass die Steigung einer Geraden gegeben ist und die Steigung einer zu senkrechten Gerade gesucht wird. Dieses Problem muss vor allem dann gelöst werden, wenn die Gleichung einer orthogonalen Gerade aufgestellt werden soll.

Gegeben:       

Gesucht:         

Gegeben ist also die Steigung . Die zwei Geraden und sollen zueinander senkrecht (orthogonal) sein. Die Steigung muss berechnet werden. Dazu verwenden wir die oben gezeigte Formel für orthogonale Geraden und stellen sie nach um:

∣

(für

Anmerkung:Die Steigung darf nicht Null sein, da die Division durch Null nicht definiert ist. Anschaulich bedeutet dies, dass die Gerade nicht waagrecht liegen darf. Die zu einer waagrechten Gerade orthogonal liegende Gerade wäre eine Parallele zur y-Achse, also eine im Koordinatensystem senkrecht liegende Gerade, die jedoch keine Funktion darstellt. Erinnere dich:Eine Funktion ordnet jedem x genau ein y zu. Bei einer Parallele zur y-Achse ist das nicht erfüllt.

1.    Bsp.:  Gegeben:   

Gesucht:   

Man könnte in die Formel einsetzen und dann nach umstellen. Oder man setzt in die bereits nach umgestellte Variante dieser Formel ein:

Wenn du nun die beiden Steigungen und miteinander vergleichst, wird dir sicher auffallen, dass die Vorzeichen umgekehrt und Zähler mit Nenner vertauscht sind.

Dein Mathelehrer wird diesen Sachverhalt wahrscheinlich folgendermaßen formulieren:„Bei orthogonalen Geraden ist die Steigung der einen Gerade der negative Kehrwert der Steigung der anderen Geraden.“ Wenn ein Mathematiker erklären soll, wie man die Steigung einer zu orthogonalen Geraden berechnet, wenn gegeben ist, wird er vermutlich zu dir sagen:„ Bilde einfach den negativen Kehrwert der gegebenen Steigung !“

Man hätte das aber auch wesentlich einfacher sagen können:

Zwei Geraden sollen senkrecht zueinander sein. Die Steigung der einen Gerade ist gegeben. Um die Steigung der zweiten Gerade zu finden, nimmst du die angegebene Steigung, drehst das Vorzeichen um und vertauschst Zähler mit Nenner!

Das meint also ein Mathematiker, wenn er vom „negativen Kehrwert der gegebenen Steigung“ spricht.  Das Wörtchen „negativ“ bedeutet nichts anderes als „Vorzeichen umdrehen“. Die Anweisung „Kehrwert bilden“ bedeutet nichts anderes als, dass „der Zähler mit dem Nenner vertauscht“ werden soll.

Die Formel bedeutet daher, dass das Vorzeichen von umgedreht und Zähler mit Nenner vertauscht werden soll.

Jetzt probieren wir das ein paar Mal:

Gegeben:       

Gesucht:         

Lösung:

Gegeben:       

Gesucht:         

Lösung:

Gegeben:       

Gesucht:         

Lösung:

Dieses Prinzip braucht man auch, wenn die Geradengleichung einer orthogonalen Geraden gesucht ist. Schreibe aber immer die Formel dazu, wenn du den „Trick“ mit dem Vorzeichen-Umdrehen und Zähler-mit-Nenner-Vertauschen anwendest. Sonst könnte dein Lehrer glauben, du hättest dein Ergebnis vom Nachbarn abgeschrieben, weil er deinen Rechenweg nicht nachvollziehen kann!

---