Schwierigere Variante der Substitution
Bei dieser Variante wird eine beliebige umkehrbare Funktion 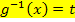 gewählt und nach
gewählt und nach 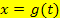 aufgelöst (oder umgekehrt
aufgelöst (oder umgekehrt 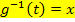 gewählt und nach t aufgelöst). Dann bildet man
gewählt und nach t aufgelöst). Dann bildet man 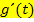 ;man leitet also
;man leitet also 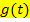 nach t ab. Als nächstes ersetzt man dx durch
nach t ab. Als nächstes ersetzt man dx durch 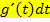 und berechnet die neuen Grenzen, indem man die ursprünglichen Grenzen in
und berechnet die neuen Grenzen, indem man die ursprünglichen Grenzen in 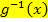 einsetzt. Nun ersetzt man im Integranden (d.h. der zu integrierenden Funktion) jedes x durch
einsetzt. Nun ersetzt man im Integranden (d.h. der zu integrierenden Funktion) jedes x durch 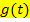 und versucht das neue Integral zu lösen.
und versucht das neue Integral zu lösen.
Puh, ziemlich kompliziert! Also noch einmal das Ganze Schritt für Schritt.
|
Anleitung zur Integration durch Substitution (Variante 2): 1. Schritt:Wähle eine beliebige umkehrbare Funktion (Stattdessen kann man auch eine beliebige umkehrbare Funktion 2. Schritt:Bilde 3. Schritt:Setze dx gleich 4. Schritt:Setze die ursprünglichen Grenzen a und b in 5. Schritt:Ersetze im Integranden (d.h. in der zu integrierenden Funktion) jedes x durch Hinweis:Bei unbestimmten Integralen entfällt der 4. Schritt. Stattdessen wird nach erfolgreicher Integration jedes auftretende t entsprechend der gewählten Substitution durch |
Als Formel geschrieben sieht das dann folgendermaßen aus:
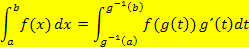
Wenn man Glück hat, ist das neue Integral leichter zu berechnen als das ursprüngliche. Das Problem daran ist, dass man zu Beginn eigentlich keine Ahnung hat, wie die Funktion 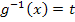 gewählt werden muss, damit letztendlich ein lösbares Integral entsteht. Das einzige, was man weißist, dass
gewählt werden muss, damit letztendlich ein lösbares Integral entsteht. Das einzige, was man weißist, dass 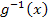 umkehrbar sein muss, denn sonst könnte man nicht eindeutig nach x auflösen. Da hilft nur eines:Ausprobieren und hoffen, dass man schnell ein geeignetes
umkehrbar sein muss, denn sonst könnte man nicht eindeutig nach x auflösen. Da hilft nur eines:Ausprobieren und hoffen, dass man schnell ein geeignetes 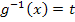 erwischt. Da man leider oft sehr unerwartete Substitutionen vornehmen muss, kann es schon ´mal viele Stunden (oder Wochen bis Monate, wenn nicht sogar Jahre!
erwischt. Da man leider oft sehr unerwartete Substitutionen vornehmen muss, kann es schon ´mal viele Stunden (oder Wochen bis Monate, wenn nicht sogar Jahre!

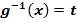 und löse sie nach x auf; das Ergebnis nennst du
und löse sie nach x auf; das Ergebnis nennst du 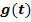 . Es gilt somit:
. Es gilt somit: 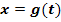
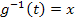 wählen und sie nach t auflösen.)
wählen und sie nach t auflösen.)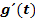 . Du musst also
. Du musst also 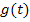 nach t ableiten.
nach t ableiten.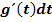 .
.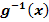 ein. Das ergibt die neuen Grenzen. Die neuen Grenzen sind somit
ein. Das ergibt die neuen Grenzen. Die neuen Grenzen sind somit 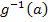 und
und 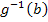 .
.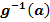 und
und 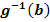 zu lösen.
zu lösen.