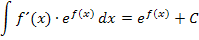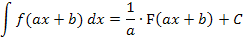1. Integration einiger Spezialfälle:Logarithmische Integration, Integration lineartransformierter Funktionen
Du solltest die einfachen Integrationsregeln (Siehe:Unbestimmtes Integral) kennen, bevor du dich mit den nachfolgenden Integrationsregeln beschäftigst.
Folgende besondere Integrationsregeln brauchst du zusätzlich zu den einfachen Integrationsregeln im Abitur:
|
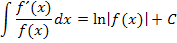
Komplizierte Integrale von Produkten, Quotienten oder verketteter Funktionen, die im Abitur in Bayern verlangt werden, lassen sich immer auf einen dieser Spezialfälle zurückführen.
Eine Ausnahme bilden Integrale von Quotienten, deren Nenner keine Summe oder Differenz ist:Solche Integrale kann man berechnen, indem man jeden Summand des Zählers einzeln durch den Nenner teilt. Nach Anwendung des Potenzgesetzes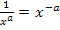 
kommt man auf ein Integral, das sich mit den einfachen Integrationsregeln lösen lässt. (Näheres dazu bei:Die Stammfunktion F(x) und einfache Integrationsregeln) Bei allen anderen Quotienten kommt nur die Verwendung der Formel 
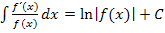in Frage.
Schauen wir uns nun die neuen Regeln der Reihe nach an. Wir beginnen mit der obersten Regel.
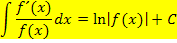
Dies bezeichnet man als „logarithmische Integration“.
Du willst wissen, woher diese Regel kommt?
Dann überlege dir, wie man zum Beispiel die Funktion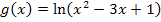 
nicht integriert, sondern ableitet. Man verwendet die Kettenregel, weil es sich um eine verkettete Funktion handelt. Die innere Funktion ist hier 
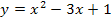;die Äußere ist der ln. Die Kettenregel besagt, dass zuerst die äußere Funktion abgeleitet werden muss. Bekanntlich ist 
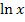abgeleitet 
. Die innere Funktion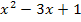 
wird an Stelle von x einfach hingeschrieben und erst später nachdifferenziert, d.h. es wird am Schluss noch mit der Ableitung der Inneren multipliziert, in diesem Fall mit 
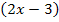. Daher ergibt sich:
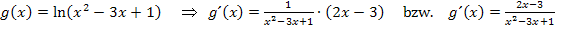
Jetzt nehmen wir eine ähnliche Funktion, zum Beispiel die Funktion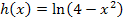 
und leiten auch sie ab. Bilde doch gleich ´mal selbst die Ableitung!
Du bist hoffentlich auf folgendes Ergebnis gekommen:
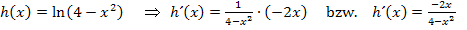
Dir ist bestimmt aufgefallen, dass sowohl bei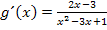 
als auch bei 
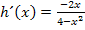im Zähler genau die Ableitung des Nenners steht.
