Weitere Integrationsregeln
Bisher haben wir uns nur mit der Integration einfacher Funktionen beschäftigt. Im Folgenden soll erklärt werden, wie sich auch bestimmte Arten komplizierterer Integrale lösen lassen. Das Ableiten einer gegebenen Funktion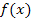 
ist im Prinzip noch ganz leicht:Zum Ableiten eines Produkts nimmt man die Produktregel, zum Ableiten eines Quotienten nimmt man die Quotientenregel, und bei verketteten Funktionen wird die Kettenregel angewendet. Leider gibt es beim Integrieren keine Regeln, die mit diesen Ableitungsregeln (Produkt-, Quotienten- bzw. Kettenregel) direkt vergleichbar sind. Man kann also nicht sagen, wenn ein Produkt vorliegt, nehme ich die Integrationsregel für Produkte, und wenn ein Quotient vorliegt, nehme ich die Regel für Quotienten. So einfach wie das Ableiten geht das Integrieren nicht. Man braucht viel Erfahrung, um schnell erkennen zu können, wie sich bei einer komplizierteren Funktion eine Stammfunktion finden lässt.
Es gibt zwar bestimmte Verfahren, die auch die Integration komplizierterer Funktionen ermöglichen. Doch müssen oft geschickte algebraische Umformungen vorgenommen werden, bevor sich eines dieser Verfahren oder eine Kombination mehrerer dieser Verfahren anwenden lässt.
| 1. Integration einiger Spezialfälle:Logarithmische Integration, Integration lineartransformierter Funktionen
2. Schwierige Integrationsregeln:Partielle Integration, Integration durch Substitution |
Bestimmte Produkte lassen sich zum Beispiel mit Hilfe der sogenannten partiellen Integration integrieren und manche verketteten Funktion mittels Integration durch Substitution. Diese beiden Integrationsverfahren stehen jedoch nicht auf dem Lehrplan für bayerische Gymnasien (G8);nur Schüler einer mathematisch-technischen FOS/BOS müssen das zum Teil im Abitur beherrschen.
Schüler, die nach dem Abitur ein Ingenieursstudium aufnehmen wollen, sollten sich trotzdem schon mit den schwierigen Integrationsregeln beschäftigen. (Man braucht sie im Studium sämtlicher Ingenieurswissenschaften.) Für alle anderen G8-Schüler reicht es völlig aus, die Spezialfälle der Integration von Produkten, Quotienten oder verketteten Funktionen zu beherrschen.
