Die Integralfunktion und der HDI
Um den folgenden Erklärungen folgen zu können, solltest du wissen, was eine Stammfunktion F(x) zu einer Funktion 
ist und wie man ein Bestimmtes Integralausrechnet. Du solltest also prinzipiell integrieren können, zumindest bei einfacheren Funktionen.
Als erstes die entscheidende Frage:Was ist überhaupt eine Integralfunktion? Ganz einfach:
Eine Integralfunktion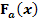 
ist eine Funktion, die sich in der folgenden Form schreiben lässt:
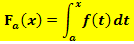
Sprich:„Integral von a bis x; f von t dt“
Andere mögliche (gleichbedeutende) Schreibweise: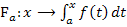 
Die Funktion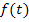 
wird dabei als Integrandenfunktion oder kurz als Integrand bezeichnet. Die Integrandenfunktion bzw. der Integrand ist also diejenige Funktion, die integriert werden soll.
Beispiel: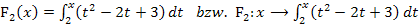 
Diese Form heißt Integraldarstellung der Integralfunktion 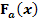. Statt 
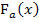ist auch die Bezeichnung F(x) gebräuchlich, also ohne den Index a. (Es gibt außerdem eine weitere Form der Integralfunktion, die sogenannte integralfreie Darstellung, also eine Form ohne Integralzeichen. Dazu später mehr.) Die Integrandenfunktion ist in diesem Beispiel die Funktion 
.
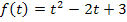Bei einer Integralfunktion ist die Variable, in der Regel x genannt, die obere Grenze. Wenn beim Integralzeichen oben die Variable x steht, ist es eine Integralfunktion.
Nur in gemeinen Aufgaben ist ausnahmsweise nicht die obere Grenze die Variable, sondern die untere. Man darf die Grenzen jedoch selbst vertauschen, wenn man gleichzeitig das Vorzeichen umdreht. Es gilt nämlich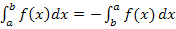 
und somit auch 
.
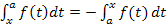In seltenen Fällen ist die Variable nicht x, sondern ein anderer Buchstabe z. B. u oder a. Dann steht aber in der Klammer hinter der Bezeichnung der Integralfunktion, also hinter F, G oder H, genau dieser Buchstabe. Z.B.: 
Auch G(u) und H(a) sind Integralfunktionen. Bei G ist u die Variable, d.h. u entspricht x. Bei H ist a die Variable, d.h. a entspricht x.
Andere mögliche Schreibweise: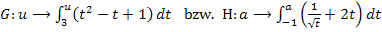 
In dieser Schreibweise erkennst du die Variable daran, dass sie vor dem Pfeil steht.
