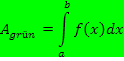Das bestimmte und das unbestimmte Integral
Das bestimmte Integral:
Zur Berechnung der Fläche zwischen dem Graph einer Funktion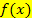 
, der x-Achse und den senkrechten Geraden 
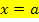und 
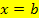benötigt man das sogenannte bestimmte Integral 
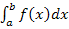. (Sprich:„Integral von a bis b von 
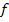von x dx“) Wenn die Funktion 
oberhalb der x-Achse verläuft oder zumindest die gesuchte Fläche oberhalb der x-Achse liegt, entspricht das bestimmte Integral 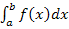der Fläche zwischen der Funktion , der x-Achse und den senkrechten Geraden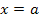 
und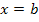 
, wenn 
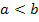gilt. Die Funktion , die hinter dem Integralzeichen steht, heißt Integrandenfunktion oder kurz Integrand. Selten wird auch als Randfunktion bezeichnet, da sie den oberen oder unteren Rand der Fläche darstellt.
Der Ausdruck „dx“, der beim Integral immer hinter die Funktionsgleichung geschrieben wird, gibt an, dass nach x integriert werden muss;d.h. dass x die Variable ist.
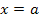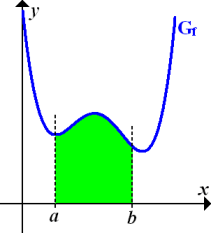
a stellt die untere Grenze des Integrals und b die obere Grenze des Integrals dar. Das bedeutet anschaulich, dass die senkrechte Gerade die Fläche auf der linken Seite begrenzt und die zweite senkrechte Gerade 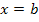die Fläche auf der rechten Seite begrenzt, vorausgesetzt es gilt a <b. Vergleiche Skizze!
 |
|
Das bestimmte Integral entspricht aber nur dann der Fläche zwischen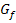 
und der x-Achse, wenn die Fläche vollständig oberhalb der x-Achse liegt;das Integral ist dann auf jeden Fall positiv. Liegt die Fläche dagegen unterhalb der x-Achse, wäre das bestimmte Integral 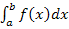negativ. Eine Fläche kann bekanntlich keinen negativen Flächeninhalt besitzen. Daran siehst du, dass das bestimmte Integral und die Fläche zwischen und der x-Achse nicht immer das Gleiche ist.
Das Integral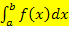 
entspricht genau genommen der sogenannten Flächenbilanz. Dabei werden diejenigen Flächenanteile positiv gewertet, die oberhalb der x-Achse liegen, und die Flächenanteile negativ gewertet werden, die unterhalb der x-Achse liegen. Sind die Flächenanteile unterhalb der x-Achse genauso großwie die oberhalb, so ist die Flächenbilanz gleich Null und somit auch das entsprechende bestimmte Integral. Wir werden nachher noch näher darauf eingehen.
Nun möchtest du aber sicher erst einmal wissen, wie man ein bestimmtes Integral ausrechnet. Damit du den folgenden Teil verstehen kannst, solltest du wissen, wie man bei einfachen Funktionen eine Stammfunktion berechnet. Wenn du das noch nicht kannst, oder wenn du gar nicht weißt, was eine Stammfunktion ist, bitte erst den Teil Die Stammfunktion F(x) und einfache Integrationsregelndurcharbeiten.
