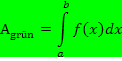1. Flächenberechnungenmit Hilfe von Integralen
Wir müssen zwei Fälle unterscheiden: Fläche zwischen Funktionsgraph und x-Achse oder Fläche zwischen zwei verschiedenen Funktionsgraphen
1.1 Fläche zwischen Funktionsgraph und x-Achse
Bei manchen Aufgaben sind die Integrationsgrenzen bereits angegeben. Dann heißt es, man soll die Fläche zwischen dem Graph der Funktion 
und der x-Achse berechnen, die zwischen den Geraden x = a und x = b liegt. Aber Vorsicht:Hat die Funktion zwischen x = a und x = b eine Nullstelle, muss das Integral an dieser Nullstelle aufgeteilt werden! (Wir werden uns nachher ein konkretes Beispiel dazu anschauen.)
Zuerst betrachten wir den einfacheren Fall, dass die Funktion zwischen x = a und x = b keine Nullstelle besitzt. Nun kommt es darauf an, ob der Funktionsgraph von im Integrationsbereich vollständig oberhalb der x-Achse liegt, vollständig unterhalb oder teils oberhalb und teils unterhalb.
1.1.1 Fläche zwischen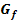 
und x-Achse im Integrationsbereich komplett oberhalb der x-Achse
Liegt die gesuchte Fläche vollständig oberhalb der x-Achse, dann entspricht das bestimmte Integral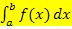 
genau der gesuchten Fläche. Dabei gilt: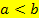 
Die kleinere Zahl a ist die untere Grenze des Integrals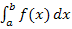 
und die größere Zahl b die obere Grenze. Das bedeutet anschaulich, dass die senkrechte Gerade 
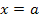die Fläche auf der linken Seite begrenzt und die zweite senkrechte Gerade 
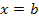die Fläche auf der rechten Seite begrenzt. Vergleiche Skizze unten! Wir integrieren also von links nach rechts.
Manchmal sind die Integrationsgrenzen bereits in der Aufgabenstellung gegeben, manchmal muss man die Grenzen selbst ermitteln.
1. Typ: Funktion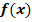 
und Grenzen x = a und x = b gegeben, mit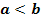 
|
|
|
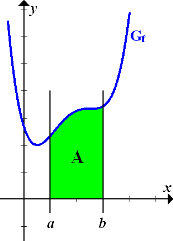
Abb.:Der Graph 
einer Funktion schließt mit der x-Achse und den Geraden x = a und x = b das Flächenstück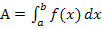 
ein. (Die Fläche liegt komplett oberhalb der x-Achse.)
Hinweis:
Überprüfe immer an Hand einer Skizze, ob die gesuchte Fläche wirklich vollständig oberhalb der x-Achse liegt, bevor du das Integral berechnest.
