Anwendungen der Integralrechnung
Notwendige Vorkenntnisse:
Du solltest wissen, was eine Stammfunktion F(x) zu einer Funktion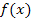 
ist und wie man F(x) zumindest bei einfacheren Funktionen f findet. Außerdem musst du bestimmte Integrale berechnen können, wenigstens von einfacheren Funktionen f. Ausführliche Erklärungen dazu in den Teilen:Die Stammfunktion F(x) und einfache Integrationsregelnsowie Das bestimmte und das unbestimmte Integral
Die Anwendungen der Integralrechnung sind vielfältig. So lassen sich besonders Flächen zwischen einer Funktion und der x-Achse oder zwischen zwei Funktionen sehr gut mit Hilfe des bestimmten Integrals berechnen. Davon leiten sich andere Anwendungen, wie die Mittelwertberechnung oder die Volumenberechnung von Rotationskörpern ab.
In der Mathematik für Ingenieure finden sich Integrale in vielen weiteren Formeln, so zum Beispiel bei der Berechnung von Flächenschwerpunkten und Bogenlängen. Doch dies würde hier zu weit führen.
Wir wollen hier nur einige für das Abitur relevante Anwendungen von Integralen besprechen.
| Übersicht über den Stoff des Teils „Anwendungen der Integralrechnung“ nach Wichtigkeit für das Mathe-Abitur geordnet:
1. Flächenberechnungen mit Hilfe von Integralen 1.1 Fläche zwischen Funktionsgraph und x-Achse
1.2 Fläche zwischen zwei Funktionsgraphen 2. Berechnungen von Mittelwerten mit Hilfe von Integralen (z. B. mittlere = durchschnittliche Geschwindigkeit oder Tagestemperatur) 3. Volumenberechnungen von Rotationskörpern mit Hilfe von Integralen 3.1 Rotation eines Graphen 3.2 Rotation eines Graphen |
1.1.1 Fläche komplett oberhalb der x-Achse
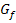um die x-Achse
