Einführung in die Integralrechnung
Die Integralrechnung gehört mit der Differenzialrechnung zur sogenannten Analysis, einem großen Teilgebiet der Mathematik. Das Integrieren (unmathematisch gesagt „Hochleiten“ oder „Aufleiten“) einer Funktion ist quasi das Gegenteil des Differenzierens oder Ableitens. Daher solltest du gut ableiten können, bevor du dich mit diesem Kapitel beschäftigst. (Siehe:Einfache Ableitungsregeln und Weitere Ableitungsregeln)
Die Anwendungen der Integralrechnung sind vielfältig und absolut unerlässlich für das Abitur bzw. Fachabitur in Mathe. Mit Hilfe von Integralen lassen sich beispielsweise Flächen zwischen Funktionen berechnen. Hier eine Übersicht über den gesamten Lehrstoff dieses Kapitels:
Für Schüler ab 11. Klasse G8 und 12. Klasse FOS/BOS:
- Was ist eine Stammfunktion F(x) einer Funktion
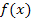 und wie findet man bei Funktionen der Form und wie findet man bei Funktionen der Form 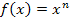 mit mit 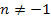 eine Stammfunktion? Wie hängt der Verlauf des Graphen eine Stammfunktion? Wie hängt der Verlauf des Graphen 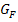 der Stammfunktion mit dem Funktionsgraphen der Stammfunktion mit dem Funktionsgraphen 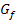 der Funktion der Funktion 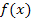 zusammen? Das wird erklärt im Teil Die Stammfunktion F(x) und einfache Integrationsregeln. zusammen? Das wird erklärt im Teil Die Stammfunktion F(x) und einfache Integrationsregeln.
Für Schüler der 12. Klasse G8 und 13. Klasse im Anschluss an FOS/BOS:
- Von der Streifenmethode zum Integral:Die Einführung des Integralzeichens und die Herleitung einiger wichtiger Grundintegrale mit Hilfe von Ober- und Untersummenbildung wird gezeigt im Teil Das Summenzeichen und die Streifenmethode. Außerdem findest du zu Beginn dieses Teils auch Erläuterungen zum bestimmten Integral
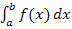 und zur Summenschreibweise und zur Summenschreibweise 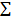 , deren Kenntnis für die Streifenmethode unerlässlich ist. , deren Kenntnis für die Streifenmethode unerlässlich ist.
Für alle Schüler einer 12 Klasse (G8, FOS, BOS):
- Was ist ein bestimmtes Integral
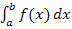 und was hat das mit der Fläche zwischen Funktionsgraph und was hat das mit der Fläche zwischen Funktionsgraph 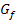 und der x-Achse zu tun? Wie berechnet man ein bestimmtes Integral (ohne Streifenmethode)? Was ist dagegen ein unbestimmtes Integral und der x-Achse zu tun? Wie berechnet man ein bestimmtes Integral (ohne Streifenmethode)? Was ist dagegen ein unbestimmtes Integral 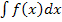 ? Antworten darauf bekommst du im Teil Das bestimmte und das unbestimmte Integral. ? Antworten darauf bekommst du im Teil Das bestimmte und das unbestimmte Integral.
- Was versteht man unter einer Integralfunktion? Was ist der Unterschied zwischen Integralfunktion und Stammfunktion? Was besagt der Hauptsatz der Differenzial- und Integralrechnung (HDI) und wie kann man Extrema oder Wendepunkte einer Integralfunktion mittels HDI berechnen? All dies wird besprochen im Teil Die Integralfunktion und der HDI.
Für Schüler der 12. Klasse G8 und mathematisch-technischer Zweig der FOS/BOS (kompletter Teil), für Schüler einer nichttechnischen FOS/BOS (nur Flächenberechnung):
- Zu den wichtigsten Anwendungen der Integralrechnung gehören die Berechnung von Mittelwerten (z.B. durchschnittliche Geschwindigkeit oder mittlere Tagestemperatur) und die Berechnung von Flächen zwischen Funktionsgraph und x-Achse sowie zwischen zwei Funktionsgraphen. Auch das Volumen eines Rotationskörpers, wie z. B. eines Zylinders, eines Kegels oder eines Sektglases, kann mit Hilfe eines Integrals ermittelt werden.
Für Schüler der 12. Klasse G8 und mathematisch-technischer Zweig der FOS/BOS:
- Das größte Problem bei der Berechnung von Integralen ist in der Regel das Finden einer Stammfunktion. Wie du auch bei schwierigeren Funktionen eine Stammfunktion finden kannst, wird erklärt im Teil Weitere Integrationsregeln. Für Schüler einer FOS/BOS (mathematisch-technischer Zweig) wird am Ende dieses Teils auch die partielle Integration und die Integration durch Substitution erklärt.
- Flächen, die sich ins Unendliche erstrecken, sind nicht immer unendlich groß! Ist eine Integrationsgrenze
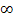 bzw. bzw. 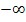 oder eine Definitionslücke, ergibt sich eine Fläche, die sich uns Unendliche erstreckt. Ob deren Flächeninhalt endlich ist oder nicht, lässt sich nur durch die Berechnung des Integrals herausfinden. Wie das gemacht wird, wird im Teil Uneigentliche Integrale erklärt. Außerdem wird hier erklärt, was es bedeutet, ob ein uneigentliches Integral konvergiert oder divergiert. oder eine Definitionslücke, ergibt sich eine Fläche, die sich uns Unendliche erstreckt. Ob deren Flächeninhalt endlich ist oder nicht, lässt sich nur durch die Berechnung des Integrals herausfinden. Wie das gemacht wird, wird im Teil Uneigentliche Integrale erklärt. Außerdem wird hier erklärt, was es bedeutet, ob ein uneigentliches Integral konvergiert oder divergiert.
Auch wenn du den Begriff „uneigentliches Integral“ im Unterricht noch nie gehört hast, solltest du dich zur Vorbereitung auf das Mathe-Abitur mit diesem Teil kurz beschäftigen, denn es werden oft Aufgaben als Transfer verlangt, die Integrale der Form 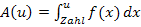 enthalten. Danach wird meist nach enthalten. Danach wird meist nach 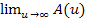 gefragt und dies entspricht letztendlich gefragt und dies entspricht letztendlich 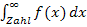 , also einem uneigentlichen Integral. , also einem uneigentlichen Integral. |

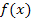 und wie findet man bei Funktionen der Form
und wie findet man bei Funktionen der Form 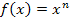 mit
mit 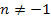 eine Stammfunktion? Wie hängt der Verlauf des Graphen
eine Stammfunktion? Wie hängt der Verlauf des Graphen 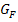 der Stammfunktion mit dem Funktionsgraphen
der Stammfunktion mit dem Funktionsgraphen 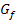 der Funktion
der Funktion 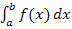 und zur Summenschreibweise
und zur Summenschreibweise 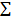 , deren Kenntnis für die Streifenmethode unerlässlich ist.
, deren Kenntnis für die Streifenmethode unerlässlich ist.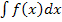 ? Antworten darauf bekommst du im Teil
? Antworten darauf bekommst du im Teil 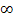 bzw.
bzw. 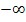 oder eine Definitionslücke, ergibt sich eine Fläche, die sich uns Unendliche erstreckt. Ob deren Flächeninhalt endlich ist oder nicht, lässt sich nur durch die Berechnung des Integrals herausfinden. Wie das gemacht wird, wird im Teil
oder eine Definitionslücke, ergibt sich eine Fläche, die sich uns Unendliche erstreckt. Ob deren Flächeninhalt endlich ist oder nicht, lässt sich nur durch die Berechnung des Integrals herausfinden. Wie das gemacht wird, wird im Teil 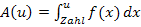 enthalten. Danach wird meist nach
enthalten. Danach wird meist nach 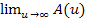 gefragt und dies entspricht letztendlich
gefragt und dies entspricht letztendlich 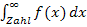 , also einem uneigentlichen Integral.
, also einem uneigentlichen Integral.