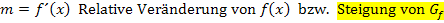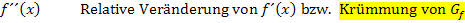Zweite Ableitung f´´(x)
Bisher ist dir die erste Ableitung  einer Funktion
einer Funktion  bekannt. Die erste Ableitung beschreibt bekanntlich die relative Veränderung des Funktionswerts
bekannt. Die erste Ableitung beschreibt bekanntlich die relative Veränderung des Funktionswerts  im Vergleich zum x, d.h.
im Vergleich zum x, d.h.  entspricht der Tangentensteigung der Funktion
entspricht der Tangentensteigung der Funktion  .
.
Leitet man die erste Ableitung nach den bekannten Ableitungsregeln (Siehe:Einfache Ableitungsregelnund Weitere Ableitungsregeln) ein weiteres Mal ab, erhält man die zweite Ableitung  . Sie entspricht der relativen Veränderung der Ableitung
. Sie entspricht der relativen Veränderung der Ableitung  im Vergleich zum x, d.h.
im Vergleich zum x, d.h.  entspricht der relativen Veränderung der Steigung von
entspricht der relativen Veränderung der Steigung von  . Doch was bedeutet das? Was kannst du dir unter der relativen Veränderung der Steigung anschaulich vorstellen? Ganz einfach:Die Veränderung der Steigung des Funktionsgraphen
. Doch was bedeutet das? Was kannst du dir unter der relativen Veränderung der Steigung anschaulich vorstellen? Ganz einfach:Die Veränderung der Steigung des Funktionsgraphen  entspricht der Krümmung von
entspricht der Krümmung von  .
.
Die zweite Ableitung 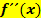 einer Funktion
einer Funktion 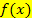 beschreibt somit die Krümmung des Graphen
beschreibt somit die Krümmung des Graphen 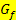 .
.
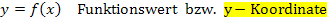
|
Wenn man sich vorstellt, man würde beispielsweise mit einem Fahrrad von links nach rechts, also in Richtung zunehmender x-Werte, auf dem Funktionsgraphen entlang fahren, kommt es darauf an, in welche Richtung man lenken müsste, um dem Verlauf des Graphen zu folgen. Lenkst du dabei nach links, sagt man der Graph ist linksgekrümmt;lenkt man umgekehrt nach rechts, ist der Graph rechtsgekrümmt.

Beachte, dass die Krümmung nicht damit zusammenhängt, ob der Graph fällt oder steigt! Es geht nur darum, in welche Richtung man lenken muss, um dem Kurvenverlauf zu folgen.
Eine Funktion muss nicht einheitlich links- oder rechtsgekrümmt sein. Bei vielen Funktionen ändert sich das Krümmungsverhalten.
An der Stelle, wo man von links nach rechts bzw. umgekehrt umlenkt, liegt ein sogenannter Wendepunkt (WEP oder WP) vor. Genau im Wendepunkt ist der Funktionsgraph somit weder links- noch rechtsgekrümmt. Außerdem sind die Wendepunkte einer Funktion  auch diejenigen Punkte, wo der Graph
auch diejenigen Punkte, wo der Graph  lokal am steilsten oder flachsten verläuft.
lokal am steilsten oder flachsten verläuft.
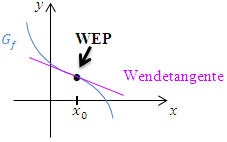
Abb.: Graph
|
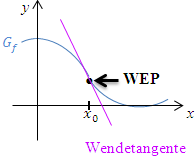
Abb.: Graph Wendetangente
|
Dass der Wendepunkt genau derjenige Punkt ist, wo sich die Krümmung ändert, dürfte an sich klar sein. Genau an dieser Stelle müsste man umlenken, wenn man auf dem Graphen entlang fahren würde. (Denk daran, dass du in Gedanken immer von links nach rechts fährst.) In der linken Abbildung müsste man zuerst nach links lenken. Am Wendepunkt lenkt man dann um und ab dort würde man nach rechts lenken. In der rechten Abbildung ist es genau umgekehrt. Zuerst müsste man nach rechts lenken und am Wendepunkt nach links umlenken. Zu beachten ist des Weiteren, dass sich der Graph  am Wendepunkt von der einen Seite kommend an die Wendetangente anschmiegt und von der anderen Seite wieder wegführt. Dies ist wirklich nur bei Wendepunkten der Fall;bei allen anderen Punkten kommt der Graph von einer Seite an die Tangente heran und geht auch auf derselben Seite wieder weg.
am Wendepunkt von der einen Seite kommend an die Wendetangente anschmiegt und von der anderen Seite wieder wegführt. Dies ist wirklich nur bei Wendepunkten der Fall;bei allen anderen Punkten kommt der Graph von einer Seite an die Tangente heran und geht auch auf derselben Seite wieder weg.