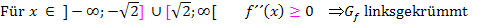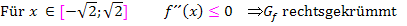Hinweis zu den Krümmungsintervallen

Nur für Schüler einer FOS (in Bayern):

Hier noch einmal die fertige Krümmungstabelle der Funktion 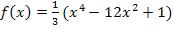von oben.

x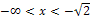
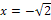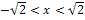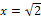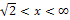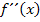	+	0		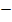0	+
	links-gekrümmt	WEP	rechts-gekrümmt	WEP	links-gekrümmt

Wenn in der Aufgabenstellung außerdem auch nach den „größtmöglichen Krümmungsintervalle“ der Funktion gefragt wäre, müßtest du zusätzlich zur Krümmungstabelle Folgendes schreiben:

Krümmungsintervalle

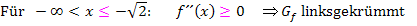
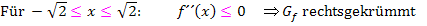
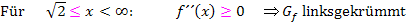
Was in der Tabelle untereinander in den jeweiligen Spalten steht, wird dabei im Prinzip nebeneinander geschrieben. Statt Plus schreibst du aber bei den Krümmungsintervallen 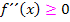und anstatt Minus entsprechend 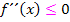. Beachte, dass du die Ränder dabei miteinschließen musst! D.h. dass du außer bei 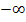und 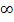bei den Krümmungsintervallen immer das Kleiner-Gleich-Zeichen bei den Rändern setzen musst anstatt des Kleiner-Zeichens in der Krümmungstabelle! Das ist auf der FOS in Bayern definitiv so verlangt! (Mit den Krümmungsintervallen ist das so ähnlich wie bei den Monotonieintervallen. Du weißbestimmt:Auch bei den Monotonieintervallen müssen auf der FOS die Ränder jeweils miteingeschlossen werden.)

Anmerkung des Autors:Das Einschließen der Ränder bei den Monotonie- und Krümmungsintervallen ist meiner persönlichen Meinung nach mathematisch unkorrekt. Wenn man jeweils die Ränder der Krümmungsintervalle in allen Intervallen miteinschließt, ergibt sich die Aussage, dass die Funktion an den jeweiligen Rändern gleichzeitig links- und rechtsgekrümmt ist. In unserer Aufgabe ergibt sich dadurch beispielsweise die Aussage, dass die Funktion an der Stelle 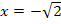gleichzeitig sowohl links- als auch rechtsgekrümmt ist. Das kann ja wohl nicht sein! Dasselbe Problem liegt bei 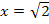vor. Wie kann denn eine Funktion an ein und derselben Stelle gleichzeitig links- und rechtsgekrümmt sein? Das kann doch gar nicht stimmen, denn an den Stellen 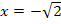und 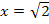ist die Funktion in Wahrheit weder links- noch rechtsgekrümmt, dort ist die Krümmung nämlich gleich Null. Laut Definition ist aber eine Funktion in einem Intervall I linksgekrümmt, wenn für alle x I die Bedingung 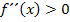gilt, und nicht für 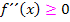. Entsprechend ist eine Funktion laut Definition in einem Intervall I rechtsgekrümmt, wenn für alle x I die Bedingung 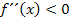gilt, und nicht für 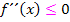. Die Schreibweise, die bei den Krümmungsintervallen auf der FOS verlangt wird, also die Aussagen „ 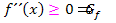linksgekrümmt“ und „ 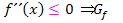rechtsgekrümmt“ sind daher für mich persönlich falsch. Es ist für mich nicht nachvollziehbar, warum dies auf der FOS derart geschrieben werden muss. (Auf dem Gymnasium oder an der Uni würde dabei genau das Zeichen 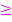bzw. 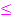in Kombination mit der Folgerung links- bzw. rechtsgekrümmt als Fehler angestrichen werden.) Ich kann dir daher leider nicht erklären, warum du das auf der FOS so schreiben musst.

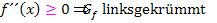Sicher ist aber auf jeden Fall:Alle Schüler einer FOS in Bayern müssen bei der Frage nach den Krümmungsintervallen einer Funktion die Ränder in jeweils allen Intervallen einschließen und bzw. 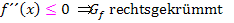schreiben. Wenn du es anders machst und die Grenzen ausschließt, also eigentlich mathematisch korrekt schreibst, gibt es Punktabzug! Ich kann dir also bloßden guten Rat geben, das Ganze nicht weiter zu hinterfragen und die Krümmungsintervalle einfach mit eingeschlossenen Rändern hinzuschreiben. (Nur die Ränder Unendlich und Minus-Unendlich bleiben auch auf der FOS ausgeschlossen, weil es sich dabei nicht um reelle Zahlen handelt. Unendlich und Minus-Unendlich werden immer ausgeschlossen, egal um was es geht.) Du musst also die Intervalle aus der Krümmungstabelle entnehmen, aber die Ränder durch die Verwendung des Kleiner-Gleich-Zeichens an Stelle des Kleiner-Zeichens jeweils einschließen.

Die beiden Bereiche, wo der Graph linksgekrümmt ist, können auch zusammengefasst geschrieben werden. Das sieht dann folgendermaßen aus:

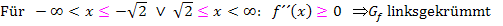
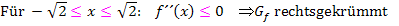
Alternativ dazu kannst du auch die Intervallschreibweise bei der Angabe der Krümmungsintervalle verwenden. Dabei musst du die eckigen Klammern bei den Krümmungsintervallen jeweils zu der Zahl hin gerichtet schreiben, außer bei Plus- und Minus Unendlich.

---