Kurzwiederholung der grundlegenden Ableitungsregeln
Du hast schon gelernt, wie du Funktionen mit Hilfe der einfachen Ableitungsregeln ableiten kannst. Dabei wurden die folgenden Regeln verwendet:
(Faktorregel)
(Summenregel)
Ausführliche Erläuterungen dieser Regeln findest du im Teil:Einfache Ableitungsregeln
Man darf also bei Summen bzw. Differenzen jeden Summanden einzeln ableiten. Einfach bei jedem Faktor den Exponenten nach vorne ziehen und mit der Zahl davor multiplizieren, außerdem vom Exponenten 1 abziehen. Zahlen ganz ohne x, die addiert oder subtrahiert werden, sogenannte additive Konstanten, fallen beim Ableiten komplett weg.
Bsp.: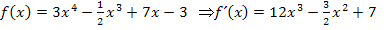 
Im Gegensatz dazu darf man bei Produkten und Quotienten nicht jeden Faktor bzw. Zähler und Nenner einzeln ableiten. Deshalb musstest du bisher ein Produkt, das in mehreren Faktoren die Variable x enthält, vor dem Ableiten ausmultiplizieren.
Bsp.: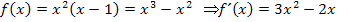 
Doch das Ausmultiplizieren ist nicht bei allen Funktionen möglich. Was wäre zum Beispiel mit der Funktion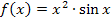 
? Das lässt sich schließlich nicht ausmultiplizieren. Um eine derartige Funktion abzuleiten, braucht man dann die Produktregel. (Genaueres dazu folgt noch.)
Eine Ausnahme bilden Zahlen ohne x, die vor einer Klammer stehen. Solche Zahlen braucht man nicht in die Klammer hineinmultiplizieren:Zahlen ohne x, die mit etwas multipliziert werden oder durch die dividiert wird, sogenannte multiplikative Konstanten, werden beim Ableiten einfach abgeschrieben.
Bsp.: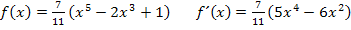 
Im Folgenden werden wir besprechen, wie man auch Produkte, die sich nicht ausmultiplizieren lassen, Quotienten und verkettete Funktionen (d.h. ineinander verschachtelte Funktionen) ableitet. Auf die Herleitungen der entsprechenden Regeln mittels Differenzialquotienten wird hier absichtlich verzichtet, da du sie sowieso nicht brauchst. Extrem wichtig sind dagegen die Ableitungen der folgenden Grundfunktionen:
(Stoff 11. Klasse G8, 2. Halbjahr)
(Stoff 11. Klasse G8, 2. Halbjahr)
(Stoff 11. Klasse G8, 2. Halbjahr)
