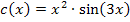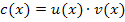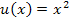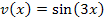Kombinationen der verschiedenen Ableitungsregeln

Im Folgenden werden wir die verschiedenen Ableitungsregeln miteinander kombinieren. Ab jetzt wird es deutlich komplizierter. Aber es hilft nichts, du brauchst das für das Abitur!

8. Bsp.:Differenziere!

a.)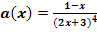

b.)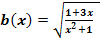

c.)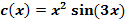

d.)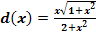

e.)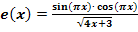

Lösung:

Zu 8a.)

Um die Funktion 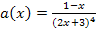abzuleiten, braucht man die Quotientenregel, weil die Funktion insgesamt ein Quotient mit x im Nenner ist. Laut Quotientenregel gilt für die Ableitung eines Bruchs mit x im Nenner:

Zähler abgeleitet mal Nenner minus Zähler mal Nenner abgeleitet und das Ganze dividiert durch den Nenner zum Quadrat.

Um bei 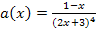die Ableitung des Nenners zu bilden benötigt man aber auch die Kettenregel. Wir beginnen also gemäßder Quotientenregel, wobei wir aber zusätzlich die Kettenregel beim Ableiten des Nenners verwenden müssen.

Quotient: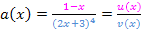

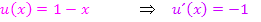
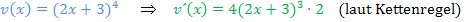
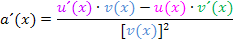
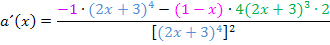
Dieser Term muss natürlich noch vereinfacht werden. Dazu klammern wir im Zähler den Faktor 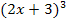aus. Dadurch ergibt sich im Zähler ein Produkt, so dass man dann kürzen darf.

Ausklammern des Faktors 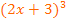liefert:

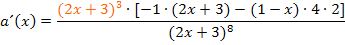
Vereinfachung des Terms innerhalb der eckigen Klammern ergibt:

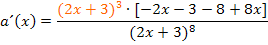
Kürzen mit :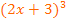

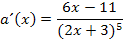
Weiter lässt sich die Ableitung nicht vereinfachen. Fertig!

Zu 8b.)

Hier noch einmal die Funktion, die abgeleitet werden soll: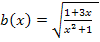

Es handelt sich hier um eine verkettete Funktion. Wir beginnen also mit der Kettenregel. Die äußere Funktion ist die Wurzel, die innere der Bruch. Laut Kettenregel müssen wir zuerst die äußere Funktion, also die Wurzel, ableiten und dabei den Bruch stehen lassen. Dann muss noch mit der Ableitung der inneren Funktion, also mit der Ableitung des Bruchs, nachdifferenziert werden. Um den Bruch abzuleiten, benötigt man des Weiteren die Quotientenregel, weil im Nenner des Bruchs die Variable x vorkommt.

Wegen 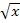abgeleitet ist 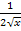, gilt entsprechend: 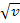(nach v) abgeleitet ist .

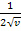Da v hier aber für die innere Funktion 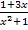steht, muss mit v´ nachdifferenziert, also mit der Ableitung des Bruchs multipliziert werden. Es gilt somit:

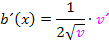
Mit 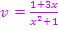und 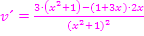erhält man:

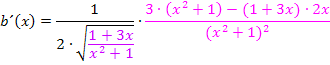
Diesen Ausdruck müssen wir natürlich noch vereinfachen.

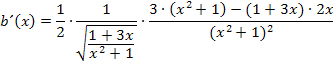
Wir teilen durch 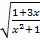 , indem wir mit dem Kehrwert 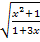multiplizieren. (Das darf man auch, wenn der Bruch unter der Wurzel steht.)

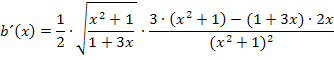
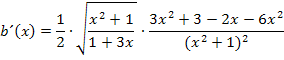
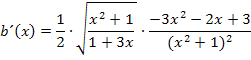
Jetzt schreiben wir noch alles, bis auf den Faktor 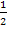, unter eine gemeinsame Wurzel. Dazu müssen sowohl Zähler als auch Nenner des hinteren Bruchs quadriert werden.

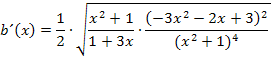
Einmal lässt sich nun der Faktor 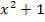kürzen.

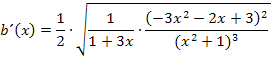
Man kann den Radikand (= Ausdruck unter der Wurzel) natürlich auch auf einen gemeinsamen Bruchstrich schreiben.

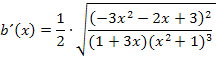
Die Klammern werden nicht aufgelöst, da sich die Ableitung dadurch bloßschlechter gleich Null setzen und nach x auflösen ließe. Somit sind wir fertig.

Zu 8c.)

Hier noch einmal die Funktionsgleichung: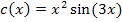

Diese Funktion ist ein Produkt;in beiden Faktoren kommt x vor. Deshalb brauchen wir die Produktregel, um sie abzuleiten. Es gilt:

---