Die Quotientenregel
Du wendest die Quotientenregel nur an bei Funktionen, die im Nenner die Variable x enthalten. Im Zähler der Funktion kann x vorkommen, muss aber nicht. Wir schreiben diese Funktionen dennoch allgemein als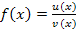 
.
Quotientenregel:
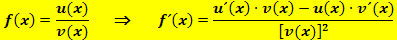
Die Regel steht auch auf deiner Merkhilfe, du kannst sie also immer nachschauen. Besser ist es natürlich, wenn du sie dir auswendig merkst, z. B. in der Kurzform:
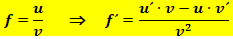
Manche Lehrer(innen) erklären die Quotientenregel auch mit dem Merksatz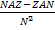 
(sprich:„Natz minus Za(h)n durch N Quadrat“) Merken kann man sich dies sicher ganz leicht, aber man muss dabei natürlich wissen, wie das gemeint ist. Mit Z ist der Zähler der Funktion gemeint, mit N natürlich der Nenner. Mit NAZ ist gemeint „Nenner mal Ableitung des Zählers“ und nicht etwa „Nennerableitung mal Zähler“. Entsprechend bedeutet ZAN „Zähler mal Ableitung des Nenners“ und nicht „Zählerableitung mal Nenner“. Also Vorsicht! Bitte nur mit 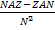arbeiten, wenn du dir hundertprozentig im Klaren darüber bist, wie das gemeint ist.
Manchen Schülern hilft die NAZ-Minus-ZAN-Regel, andere arbeiten lieber mit der u,v-Formel, die oben als erstes gezeigt wurde. Im Prinzip ist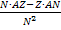 
sowieso das Selbe wie 
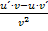. Du erkennst das sicher sofort, wenn du nur die Reihenfolge von u´und v beim ersten Produkt des Zählers vertauschst. Dann erhältst du: 
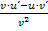Da v dem Nenner N entspricht, u´ der Ableitung des Zählers AZ, u dem Zähler Z und v´der Ableitung des Nenners AN, dürfte dir nun klar sein, dass beide Formeln gleichbedeutend sind. Die Quotientenregel steht, wie auch die Produktregel, auf der Merkhilfe;du kannst sie also zur Not auch immer schnell nachschauen. Der Zähler der Quotientenregel ist sehr ähnlich der Produktregel, unterscheidet sich aber im Rechenzeichen in der Mitte:Bei der Quotientenregel steht ein Minus, bei der Produktregel dagegen ein Plus. Das kann man leicht man durcheinander bringen. Bei Unsicherheiten immer besser noch einmal in der Merkhilfe nachschauen!
Wir werden auf dieser website im Folgenden immer die Form mit u und v, die auch auf der Merkhilfe steht, verwenden und nicht die NAZ-Minus-ZAN-Regel.
Nun gleich zu einigen Beispielen für die Anwendung der Quotientenregel.
4. Bsp.: Differenziere folgende Funktionen! (Vereinfache die Ableitung jeweils soweit möglich.)
a.)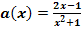 
b.)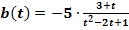 
c.)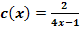 
d.)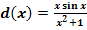 
e.)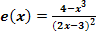 
f.)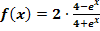 
(Nur für Schüler, die im Unterricht 
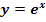bereits behandelt haben)
g.)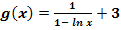 
(Nur für Schüler, die in der Schule 
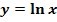schon gelernt haben)
Lösung:
Zu 4a.)
Um die Funktion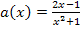 
abzuleiten, benötigt man die Quotientenregel, da im Nenner x vorkommt. Bei Funktionen, deren Nenner dagegen kein x enthält, wird beim Ableiten nicht die Quotientenregel angewendet. Nehmen wir zum Beispiel die Funktion 
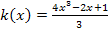, welche offensichtlich kein x im Nenner enthält. Statt 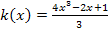könnte man auch 
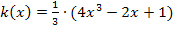schreiben. Die Konstante 
bleibt beim Ableiten einfach außerhalb der Klammer stehen, da es sich um eine Zahl handelt, die multipliziert wird, und solche Zahlen bleiben beim Ableiten bekanntlich immer stehen.
