Die Kettenregel

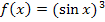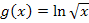Man verwendet sie beim Ableiten von verketteten Funktionen, d.h. bei Funktionen, die ineinander verschachtelt sind wie zum Beispiel oder . Bei diesen Funktionen ist jeweils eine Funktion in eine andere Funktion für x eingesetzt worden. Bei der Funktion 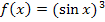ist beispielsweise die Funktion 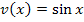in die Funktion 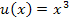eingesetzt. Man sagt, 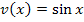und 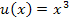sind miteinander verkettet. Die Funktion 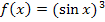lässt sich daher auch als 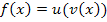ansehen. 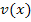ist dabei die innere Funktion;sie wurde in die äußere Funktion 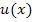für x eingesetzt.

Achtung:Unterscheide genau zwischen 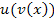, sprich „u von v von x“, und 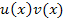, sprich „u von x mal v von x“! 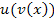steht für die Verkettung und nicht für ein Produkt! 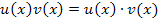beschreibt dagegen das Produkt der beiden Funktionen 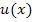und 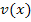. Wie man das Produkt zweier Funktionen ableitet, haben wir vorher bei der Produktregel bereits besprochen. (Genaueres dazu bei:Die Produktregel)

Statt der Schreibweise 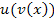für die Verkettung von u mit v ist auch die Schreibweise 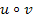(sprich:u verkettet mit v) gebräuchlich. Dabei steht vor dem Kringel immer die äußere Funktion und hinter dem Kringel die innere Funktion. 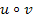bedeutet also, dass v in u eingesetzt ist und nicht umgekehrt u in v. Es ist hier genau zwischen innerer Funktion und äußerer Funktion zu unterscheiden!

Um dir das Prinzip des Verkettens zweier Funktionen näher zu bringen, folgt nun eine kleine Vorübung, die noch nicht direkt mit der Ableitung zu tun hat. Wenn wir nachher verkettete Funktionen ableiten, ist die verkettete Funktion bereits gegeben. Du musst sie nicht selbst bilden, aber du musst selbstständig erkennen können, was jeweils innere und äußere Funktion ist. Die Funktion ist nachher also bereits verkettet angegeben und muss nicht von dir verkettet, sondern nur abgeleitet werden. Dennoch wollen wir vorweg eine Übung machen, bei der du selbst zwei gegebene Funktionen miteinander verketten sollst.

Vorübung zum Verketten:  Bilde jeweils 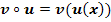und 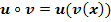mit den im Folgenden gegebenen Funktionen!

a.)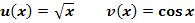

b.)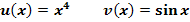

c.)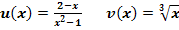

d.)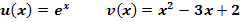

Lösung:

Zu a.)

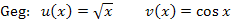
Zuerst bilden wir 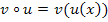. Das heißt, man muss 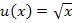(innere Funktion) in 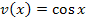(äußere Funktion) für x einsetzen.

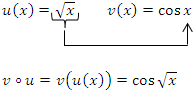
Hier ist also die Wurzel innere Funktion und der Kosinus die äußere Funktion.

Jetzt machen wir es genau anders herum. Wir bilden 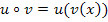. Das heißt, man muss 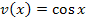(innere Funktion) in 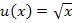(äußere Funktion) für x einsetzen.

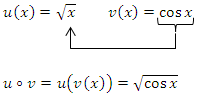
Hier ist also der Kosinus die innere und die Wurzel äußere Funktion.

Zu b.)

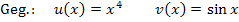
Wir beginnen wieder mit 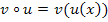. Das heißt, man muss 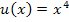(innere Funktion) in 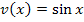(äußere Funktion) für x einsetzen.

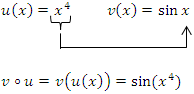
Hier ist also die Hoch-vier-Funktion innere und Sinus die äußere Funktion.

Jetzt machen wir es genau anders herum. Wir bilden 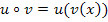. Das heißt, man muss 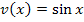(innere Funktion) in 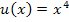(äußere Funktion) für x einsetzen.

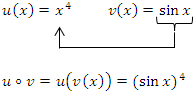
Hier ist also der Sinus die innere und die Hoch-vier-Funktion äußere Funktion. An Stelle von 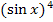kann übrigens auch 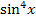geschrieben werden.

---