Ausführliche Erklärung zu u´(x) Bsp. 7d.)
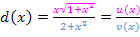
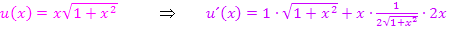
Du kannst nicht nachvollziehen, wie man auf u´(x) kommt? Dann schauen wir uns das doch ´mal genauer an.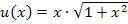 
ist offensichtlich ein Produkt, das in beiden Faktoren die Variable x enthält. Wir verwenden daher die Produktregel, um 
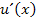zu bilden:Ersten Faktor ableiten mal zweiten stehen lassen plus ersten Faktor stehen lassen mal zweiten Faktor ableiten. Weil die Bezeichnungen u und v bereits vergeben sind für den Zähler und Nenner der Funktion 
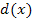müssen wir hier ausnahmsweise andere Buchstaben für den ersten bzw. zweiten Faktor des Produkts 
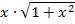verwenden. Den ersten Faktor bezeichnen wir im Folgenden mit 
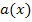, den zweiten mit 
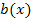. Mit diesen Bezeichnungen lautet die Produktregel:
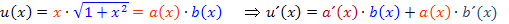
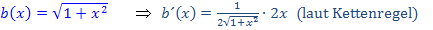
Auf die Ableitung des zweiten Faktors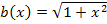 
kommt man mit Hilfe der Kettenregel, wobei die Wurzel äußere Funktion und 
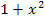die innere Funktion v ist. (Wir verwenden den Buchstaben v ab sofort nicht mehr für den Nenner der kompletten Funktion 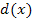, sondern für die innere Funktion bei der Kettenregel.) Bekanntlich ist 
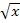abgeleitet 
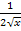. Daher ist entsprechend 
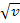(nach v) abgeleitet 
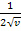. Weil v aber die von x abhängige, innere Funktion 
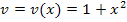darstellt, muss noch mit 
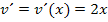nachdifferenziert werden. Es gilt: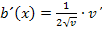 
So erhält man die oben gezeigte Ableitung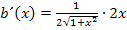 
des zweiten Faktors 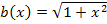, die wir bei der Produktregel brauchen. Nun wenden wir die Produktregel an.
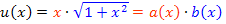
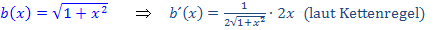
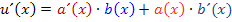
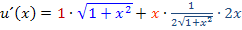
Jetzt ist dir hoffentlich klar, wie man auf die Ableitung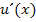 
des Zählers der Funktion 
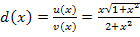kommt.
