Stetigkeit und Differenzierbarkeit
1. Anschauliche Erklärung
Über zwei mathematische Begriffe stolpert man zwangsläufig, wenn man sich mit Aufgaben aus dem Bereich der Analysis beschäftigt:Erstens über den Begriff der „Stetigkeit“ und zweitens über den Begriff der „Differenzierbarkeit“. Oft heißt es „die stetige Funktion“ oder „die stetige und differenzierbare Funktion“. Doch was bedeutet das? Vorweg eine kurze anschauliche Erklärung:Eine Funktion ist stetig, wenn sie innerhalb ihrer Definitionsmenge keine Sprungstellen hat. Eine Funktion ist differenzierbar, wenn der Graph keinen Knick hat. Jetzt aber etwas genauer.
Stetigkeit
Eine Funktion ist stetig, wenn sie innerhalb ihrer Definitionsmenge keine Sprungstellen hat. Eine Polynomfunktion hat keine Sprungstellen und ist somit immer stetig in 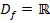 .
.
Ist eine Funktion stetig, lässt sich ihr Graph (zumindest innerhalb ihrer Definitionsmenge) zeichnen, ohne den Stift abzusetzen. Der Graph einer stetigen Funktion hat für x 
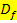 keine Sprungstellen – Knicke bzw. Spitzen kann er jedoch haben.
keine Sprungstellen – Knicke bzw. Spitzen kann er jedoch haben.
Vorsicht:Die Regel, dass eine Funktion unstetig ist, wenn sie eine oder mehrere Sprungstellen hat, gilt wirklich nur an Stellen innerhalb der Definitionsmenge! Liegt eine Sprungstelle an einer Definitionslücke, ist die Funktion dennoch stetig! Betrachte dazu auch das letzte der unten gezeigten Beispiele!
Beispiele:
 |
Die Funktion ist an der Stelle  nicht stetig. nicht stetig. |
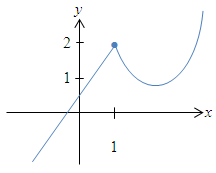 |
Die Funktion ist an der Stelle  stetig. stetig. |
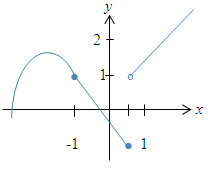 |
Die Funktion ist an der Stelle 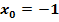 stetig, aber an der Stelle stetig, aber an der Stelle 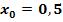 nicht stetig, weil sie dort eine Sprungstelle hat. nicht stetig, weil sie dort eine Sprungstelle hat. |
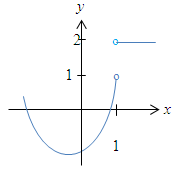 |
Vorsicht!
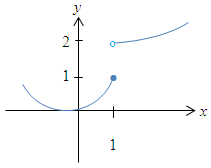
Die Funktion ist in ihrer gesamten Definitionsmenge stetig! An der Stellex = 1 ist sie gar nicht definiert (zweimal offener Kreis, kein ausgefüllter Punkt), daher interessiert diese Stelle nicht und die Funktion ist trotz Sprungstelle stetig für x |
Differenzierbarkeit
Eine Funktion ist differenzierbar, wenn ihr Graph keinen Knick bzw. keine Spitze hat, also überall „weich“ verläuft. Eine Polynomfunktion hat keinen Knick und ist somit immer differenzierbar in 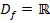 . Wenn eine Funktion in ihrer gesamten Definitionsmenge differenzierbar ist, sagt man, sie ist „global differenzierbar“. Der Graph einer global differenzierbaren Funktion verläuft also überall „weich“ bzw. „glatt“. Die Steigung der Funktion lässt sich in jedem Kurvenpunkt P berechnen. Die Steigung der Funktion
. Wenn eine Funktion in ihrer gesamten Definitionsmenge differenzierbar ist, sagt man, sie ist „global differenzierbar“. Der Graph einer global differenzierbaren Funktion verläuft also überall „weich“ bzw. „glatt“. Die Steigung der Funktion lässt sich in jedem Kurvenpunkt P berechnen. Die Steigung der Funktion 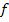 im Punkt
im Punkt 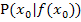 entspricht dabei der Steigung der Tangente an den Graph
entspricht dabei der Steigung der Tangente an den Graph 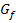 im Punkt
im Punkt 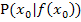 .
.
Hinweis:Mit  ist eine bestimmte Zahl gemeint.
ist eine bestimmte Zahl gemeint. 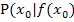 ) ist daher ein festgelegter Punkt des Graphen.
) ist daher ein festgelegter Punkt des Graphen.
Kann die Steigung der Funktion, also die Tangentensteigung, in einem bestimmten Punkt nicht angegeben werden, weil sie an dieser Stelle einen Knick hat, sagt man:Die Funktion ist an dieser Stelle nicht differenzierbar. (So eine Funktion ist natürlich nicht global differenzierbar.)
Hat der Graph der Funktion an einer bestimmten Stelle  eine Sprungstelle, d.h. sie ist an dieser Stelle nicht stetig, kann die Steigung dort natürlich auch nicht angegeben werden. Daher ist die Stetigkeit an der Stelle
eine Sprungstelle, d.h. sie ist an dieser Stelle nicht stetig, kann die Steigung dort natürlich auch nicht angegeben werden. Daher ist die Stetigkeit an der Stelle  absolute Voraussetzung für die Differenzierbarkeit bei
absolute Voraussetzung für die Differenzierbarkeit bei  . Damit eine Funktion an der Stelle
. Damit eine Funktion an der Stelle 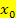 überhaupt differenzierbar sein kann, muss sie an der Stelle
überhaupt differenzierbar sein kann, muss sie an der Stelle 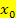 erst einmal stetig sein.
erst einmal stetig sein.

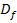 !
!