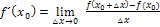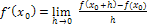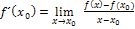Welchen Ansatz bei welchen Aufgaben verwenden
Ihr habt im Schulunterricht mehrere Varianten des Differenzialquotienten besprochen, vermutlich die Form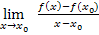 
und die h-Methode. Wenn du selbst bei einer bestimmten Aufgabe die Tangentensteigung einer gegebenen Funktion ausrechnen musst, also wenn du die Ableitung 
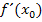oder 
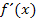einer Funktion mit dem Differenzialquotienten ermitteln sollst, musst du letztendlich immer selber entscheiden, welchen Ansatz du wählst.
Welchen Ansatz in welchem Fall nehmen?
Ist in der Aufgabe nach der Tangentensteigung 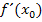an einer konkreten Stelle 
gefragt und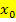 
ist wirklich als Zahl angegeben, ist es an sich egal, welchen Ansatz du für den Differenzialquotienten wählst. Alle drei Varianten funktionieren dann relativ gut.
Ist aber keine richtige Zahl für 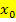gegeben, ist es geschickter Die h-Methode(oder die Delta-x-Methode) zu nehmen, um eine gegebene Funktion abzuleiten. Ist also keine richtige Zahl für gegeben, besser nicht mit 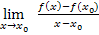rechnen, weil sich damit vor allem bei Funktionen mit 
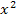und x im Funktionsterm ganz schlecht rechnen lässt.
Soll die Tangentensteigung bei einer Funktion gleich an mehreren konkret angegebenen Stellen berechnet werden, ist es geschickt, die Ableitung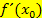 
vorweg allgemein zu ermitteln, ohne dabei eine konkrete Zahl für 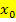einzusetzen. Das geht vor allem bei Funktionen mit 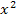und x im Funktionsterm am besten mit der h-Methode oder der Delta-x-Methode. (Bei Funktionen des Typs 
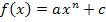funktioniert aber auch die Variante 3 ganz gut.) Erst ganz am Schluss setzt du dann nacheinander bei 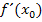jeweils die angegeben Zahlen für ein.
Wenn die Ableitungsfunktion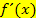 
gesucht ist, verwendest du auch am besten die h-Methode oder die Delta-x-Methode. Ob du dabei gleich zu Beginn der Rechnung rein formal durch x ersetzt oder erst am Schluss, musst du selbst entscheiden. Das ist reine Geschmackssache.
Die drei verschiedenen Formen des Differenzialquotienten im Vergleich
Bei den Ausdrücken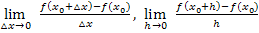 
und 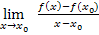handelt es sich nur um unterschiedliche Schreibweisen für den Differenzialquotienten. Damit kann jeweils die Steigung einer Kurve 
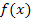, d.h. die Tangentensteigung der Funktion 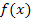, an einer bestimmten Stelle , also ihre Ableitung 
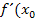), berechnet werden. Jede der drei Formen des Differenzialquotienten führt daher zum gleichen Endergebnis, nämlich der Tangentensteigung der Funktion 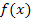an der Stelle . Wir schreiben für die Steigung der Tangente nicht mehr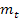 
, sondern .
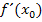Die ersten beiden Formen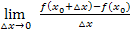 
und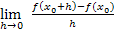 
sind im Prinzip fast gleich, denn das 
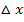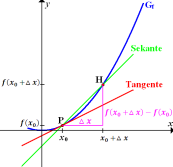
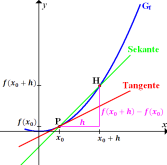
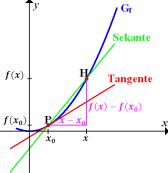
aus der ersten Schreibweise entspricht einfach dem h aus der zweiten. Mit 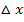bzw. h ist dabei der Unterschied der x-Koordinaten der zwei Punkte P und H bezeichnet. (Vergleiche auch nachfolgende Abbildungen Links und Mitte!) Der dritte Ansatz unterscheidet sich etwas stärker von den ersten beiden. Der Unterschied der x-Koordinaten der zwei Punkte P und H ist dabei 
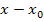. (Vergleiche Abbildung rechts!) Dennoch stellen alle drei Ausdrücke nichts anderes als den Differenzialquotienten einer Funktion 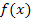an der Stelle dar.
| Delta-x-Methode:
Differenzialquotient, d.h. Tangentensteigung an der Stelle
|
h-Methode:
Differenzialquotient d.h. Tangentensteigung an der Stelle
|
Variante 3:
Differenzialquotient d.h. Tangentensteigung an der Stelle
|
Die drei Ausdrücke 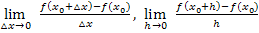und 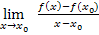werden nach demselben Prinzip hergeleitet:Man wählt zusätzlich zum gegebenen Kurvenpunkt 
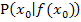jeweils einen weiteren Kurvenpunkt H als Hilfspunkt und legt eine Gerade durch die beiden Punkte P und H. Die Gerade PH ist eine Sekante des Graphen 
.
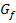