Extremwertaufgaben mit Nebenbedingung / Optimierungsprobleme
Notwendige Vorkenntnisse:Du solltest wissen, was man unter der (ersten) Ableitung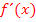 
einer Funktion 
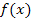versteht und wie man die Ableitung bildet. Außerdem solltest du die Extrema einer gegebenen Funktion berechnen können. Näheres dazu findest du in den Teilen:Einfache Ableitungsregeln, Die Ableitungsfunktionund Weitere Ableitungsregeln
Bisher haben wir nur Extremwertaufgaben ohne Nebenbedingungen gelöst, d.h. es war eine Funktion gegeben und man musste ihre Extrema berechnen. Dabei handelte es sich oft nur um relative (lokale) Extrempunkte und nicht um die absoluten (globalen) Extrema. Wir suchten also einfach alle Kurvenpunkte, die in einer bestimmten Umgebung am höchsten oder tiefsten lagen;es musste sich aber nicht um die allerhöchsten oder allertiefsten Punkte handeln. Das wird sich nun ändern. Im Folgenden ist immer nach dem absoluten (globalen) Minimum bzw. Maximum gefragt. Außerdem müssen wir bei den sogenannten Extremwertaufgaben mit Nebenbedingung die Funktionsgleichung erst selbst aufstellen. Diese Funktion nennen wir „Zielfunktion“. Es ist ja das Ziel vorweg diese Funktion zu ermitteln, damit wir dann ihr absolutes Minimum bzw. Maximum ausrechnen können. Das Hauptproblem bei den Extremwertaufgaben mit Nebenbedingung ist es die Zielfunktion zu finden. Wie das geht, schauen wir uns gleich an einem konkreten, relativ einfachen Beispiel an. Daran wird dann auch erklärt, was man denn überhaupt unter der „Nebenbedingung“ versteht.
Einführungsbeispiel:Koppelzaun
Wir haben 100 Meter Elektrozaun zur Verfügung. Wir wollen damit eine möglichst große, rechteckige Koppel für das Pferd Rikki umzäunen. Die Koppel soll direkt an einen geradeaus fließenden Bach anschließen. Da Rikki sowieso nicht durch den Bach geht oder darüber springt, brauchen wir auf dieser Seite keinen Zaun. Wie müssen wir dazu die Breite und Länge der Koppel wählen? Wie großist die maximale Fläche dieser Koppel? (Von zusätzlichen Komplikationen, wie zum Beispiel einem Eingangstor oder dem Mehrverbrauch des Elektrozauns beim Anbinden an den Pfosten, wollen wir dabei absehen.)
Lösung:
Zuerst fertigen wir eine Skizze der Gegebenheiten an.
Bei Extremwertaufgaben mit Nebenbedingung treten immer mehrere verschiedene unbekannte Größen auf, hier die Länge und die Breite. Vorweg muss festgelegt werden, wie sie bezeichnet werden sollen. Es bietet sich an die Länge der Koppel mit l und die Breite mit b zu bezeichnen. Wir legen daher fest:
Länge der Koppel in Metern:l
Breite der Koppel in Metern:b
Wir sollen nun l und b so berechnen, dass die umzäunte, rechteckige Fläche maximal wird.
1. Schritt:Nebenbedingung aufstellen
Die Nebenbedingung, kurz NB;ist eine Gleichung, die einen Zusammenhang zwischen den auftretenden Variablen (Unbekannten) herstellt, also hier eine Gleichung, welche die beiden Variablen l und b enthält.
Aus der Angabe ist bekannt, dass 100 m Zaun zur Verfügung stehen. Die Zaunlänge setzt sich zusammen aus zweimal der Breite b und einmal der Länge l.
