Einfache Ableitungsregeln
Die Ableitungsfunktion  , kurz auch einfach nur „Ableitung“ genannt, gibt die Steigung einer Funktion
, kurz auch einfach nur „Ableitung“ genannt, gibt die Steigung einer Funktion 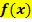 an der Stelle x an. Genauer gesagt:Die Ableitung / Ableitungsfunktion
an der Stelle x an. Genauer gesagt:Die Ableitung / Ableitungsfunktion 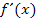 ordnet jeder Stelle x die Steigung der Funktion
ordnet jeder Stelle x die Steigung der Funktion 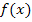 an dieser Stelle zu. Um die Steigung einer Kurve in einem bestimmten Punkt P zu berechnen, muss zuerst die Ableitung
an dieser Stelle zu. Um die Steigung einer Kurve in einem bestimmten Punkt P zu berechnen, muss zuerst die Ableitung 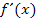 ermittelt und danach die x-Koordinate des jeweiligen Kurvenpunkts P für x in die Ableitung eingesetzt werden.
ermittelt und danach die x-Koordinate des jeweiligen Kurvenpunkts P für x in die Ableitung eingesetzt werden.
Das Berechnen von 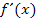 mit x als Variable nennt man globales ableiten oder auch globales differenzieren. Das Berechnen der Steigung von
mit x als Variable nennt man globales ableiten oder auch globales differenzieren. Das Berechnen der Steigung von 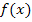 an einer bestimmten Stelle
an einer bestimmten Stelle 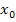 , also das Berechnen von
, also das Berechnen von 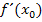 , wobei
, wobei 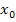 für eine konkrete feste Zahl steht, heißt dagegen lokales ableiten oder lokales differenzieren. Spricht man allgemein nur vom „ableiten“ oder „differenzieren“ einer Funktion, ist in der Regel das globale ableiten bzw. differenzieren der Funktion gemein.
für eine konkrete feste Zahl steht, heißt dagegen lokales ableiten oder lokales differenzieren. Spricht man allgemein nur vom „ableiten“ oder „differenzieren“ einer Funktion, ist in der Regel das globale ableiten bzw. differenzieren der Funktion gemein.
Aus dem vorhergehenden Kapitel wissen wir:Die Ableitung 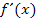 kann mit dem Differenzialquotienten berechnet werden. Das dauert aber sehr lange. Außerdem macht diese Methode vielen Schülern Schwierigkeiten. Der Differenzialquotient ist erfreulicherweise als reine Herleitung der Ableitung anzusehen.
kann mit dem Differenzialquotienten berechnet werden. Das dauert aber sehr lange. Außerdem macht diese Methode vielen Schülern Schwierigkeiten. Der Differenzialquotient ist erfreulicherweise als reine Herleitung der Ableitung anzusehen.
Wir wollen nun einen wesentlich einfacheren Weg lernen, wie man z. B. Funktionen der Form 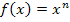 mit Hilfe der sogenannten Ableitungsregeln ableiten bzw. differenzieren kann. Für die komplette Differenzialrechnung sind die folgenden Regeln absolute Grundlage. Sie werden dich bis zum Abitur nie mehr verlassen! Eventuell brauchst du sie sogar im Studium noch. (Dazu musst du noch nicht einmal Mathe studieren. Auch in jedem Ingenieurs- oder Wirtschaftsstudiengang wird das vorausgesetzt!) Das ist also wirklich total wichtig!
mit Hilfe der sogenannten Ableitungsregeln ableiten bzw. differenzieren kann. Für die komplette Differenzialrechnung sind die folgenden Regeln absolute Grundlage. Sie werden dich bis zum Abitur nie mehr verlassen! Eventuell brauchst du sie sogar im Studium noch. (Dazu musst du noch nicht einmal Mathe studieren. Auch in jedem Ingenieurs- oder Wirtschaftsstudiengang wird das vorausgesetzt!) Das ist also wirklich total wichtig!
Auf die jeweilige Herleitung bzw. den Beweis der folgenden Formeln mittels Differenzialquotienten soll hier verzichtet werden. Die Herleitungen/Beweise brauchst du sowieso nicht.
| Allgemeine Ableitungsregeln:
|
Falls du jetzt noch nicht weißt, wie du diese Formeln anwenden kannst, keine Sorge! Das Ganze wird sofort in Worten und an Hand vieler Beispiele erklärt.
Fangen wir mit der obersten Formel an. Sie ist wohl auch die allerwichtigste Ableitungsregel.
 (mit n
(mit n  ℝ)
ℝ)
Hat eine Funktion die Form 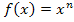 , also beispielsweise
, also beispielsweise 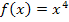 , dann lautet die Ableitung
, dann lautet die Ableitung 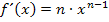 , also bei unserem Beispiel
, also bei unserem Beispiel 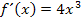 . Du musst also zuerst die Zahl, die bei
. Du musst also zuerst die Zahl, die bei 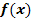 im Exponenten steht, vor das x schreiben und außerdem beim Exponenten die Zahl 1 abziehen. An den folgenden Beispielen wird dir das bestimmt gleich klar.
im Exponenten steht, vor das x schreiben und außerdem beim Exponenten die Zahl 1 abziehen. An den folgenden Beispielen wird dir das bestimmt gleich klar.
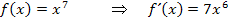
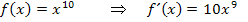
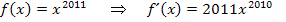
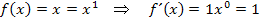 (Zur Erinnerung:
(Zur Erinnerung: 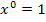 )
)
Das Prinzip müsste jetzt klar sein. Kurzer Test, ob du es soweit verstanden hast:Was ist die Ableitung von 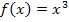 ?
?
Du bist bestimmt selbst auf das Ergebnis 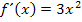 gekommen, das war ja auch nicht schwer. Leider geht das nicht immer ganz so leicht. Die Regel kann nämlich nicht nur bei Potenzen mit natürlichen Exponenten angewendet werden, sondern auch dann, wenn der Exponent eine beliebige reelle Zahl ist. Der Exponent n von
gekommen, das war ja auch nicht schwer. Leider geht das nicht immer ganz so leicht. Die Regel kann nämlich nicht nur bei Potenzen mit natürlichen Exponenten angewendet werden, sondern auch dann, wenn der Exponent eine beliebige reelle Zahl ist. Der Exponent n von 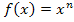 kann also auch eine negative Zahl oder ein Bruch sein.
kann also auch eine negative Zahl oder ein Bruch sein.
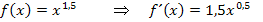
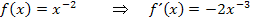
Du musst bei negativen Exponenten allerdings ganz besonders aufpassen, wenn du 1 abziehst:Wirklich 1 abziehen und nicht aus Versehen dazuzählen, d.h. du musst auf dem Zahlenstrahl in Gedanken um 1 nach links gehen!
Das ist aber an sich auch noch nicht das Problem. Die Schwierigkeit liegt dagegen oft vielmehr darin, die Funktion vorweg auf die benötigte Form 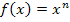 zu bringen.
zu bringen.

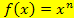

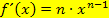


 (Faktorregel)
(Faktorregel) (Summenregel)
(Summenregel)