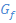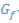Ausführliche Lösung zu Bsp. 4b.)

Hier noch einmal alle gegebenen Graphen:

Abb. 7	Abb. 8	Abb. 9
Abb. 10	Abb. 11	Abb. 12

Welcher Graph stellt die Ableitungsfunktion von welchem dar? Wir sollen moglichst viele zusammengehorige Paare von Funktion und Ableitungsfunktion finden.

Lösung:

Abb. 7 stellt die Ableitung von Abb. 9 dar.

Abb. 10 stellt die Ableitung von Abb. 12 dar.

Abb. 11 stellt die Ableitung von Abb. 8 dar.

Erklarungen zur Losung:

Wie kommt man darauf, dass nur Abb. 7 die Ableitung von Abb. 9 zeigen kann?

Betrachte noch einmal Abb. 9!

Der in Abb. 9 gezeigte Graph ist fur 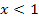eine fallende Gerade mit der Steigung -1 und fur 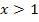eine steigende Gerade mit der Steigung +1. (Es handelt sich bei Abb. 9 ubrigens um den Graph der Funktion 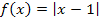, die um 1 nach rechts verschobene Betragsfunktion.) Die Ableitung entspricht bekanntlich der Steigung der Funktion. Somit muss die Ableitung der in Abb. 9 gezeigten Funktion fur 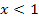konstant -1 und fur 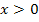konstant +1 sein. Die Ableitungsfunktion muss zwangslaufig fur 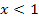die waagrechte Gerade 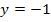und fur 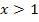die waagrechte Gerade 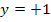sein.

An der Stelle 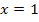ist der in Abb. 9 gezeigte Graph nicht differenzierbar, d.h. man kann die Steigung der Tangente dort nicht eindeutig ermitteln. Der Graph der in Abb. 9 gezeigten Funktion hat hier eine Spitze. Man wei?also nicht, ob an der Stelle 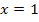fur die Steigung -1, +1 oder irgendein anderer Wert gilt. Die Ableitung ist an der Stelle 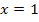deshalb nicht definiert, was zu einer Definitionslucke der Ableitungsfunktion bei 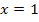fuhrt. Nun betrachte noch einmal die Abbildungen 7 bis 12!

Was stellst du dabei fest?

Nur Abb. 7 erfullt alle soeben beschriebenen Bedingungen.

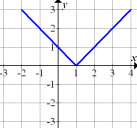
Abb. 9

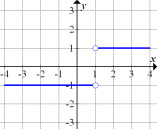
Abb. 7

Vorsicht:Abb. 10 kann nicht die Ableitung von Abb. 9 sein, da der in Abb. 10 gezeigte Graph fur 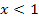die waagrechte Gerade 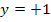und fur 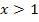die waagrechte Gerade 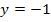zeigt. D.h. die Vorzeichen waren falsch.

Vergleiche dazu noch einmal Abb.10!

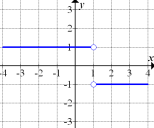
Abb. 10

Abb. 10 ist die Ableitung einer Funktion, die fur 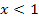 konstant mit der Steigung +1 steigt und fur 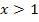konstant mit der Steigung -1 fallt. Diese Bedingung erfullt der Graph in Abb. 12. Daher stellt Abb. 10 die Ableitung von Abb. 12 dar. (In Abb. 12 ist ubrigens der Graph der Funktion 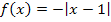dargestellt;das ist die um 1 nach rechts verschobene und an der x-Achse gespiegelte Betragsfunktion.)

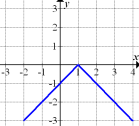
Abb. 12

Abb. 10

Wie kommt man darauf, dass Abb. 11 die Ableitung von Abb. 8 darstellt?

Betrachte dazu erst noch einmal Abb. 8!

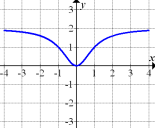
Abb. 8

Der in Abb. 8 dargestellte Graph hat bei 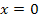eine waagrechte Tangente. Daher muss die zugehorige Ableitungsfunktion bei 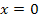eine Nullstelle besitzen. Fur 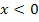fallt der Graph, so dass die zugehorige Ableitungsfunktion unterhalb der x-Achse liegen muss. Fur 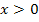steigt der Graph, so dass die zugehorige Ableitungsfunktion oberhalb der x-Achse liegen muss. Fur betragsma?ig gro?e x (ganz weit links bzw. rechts im Koordinatensystem) verlauft der in Abb. 8 gezeigte Graph immer flacher;die Steigung nahert sich an Null an. Daher muss sich die zugehorige Ableitungsfunktion fur x gegen 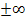an Null annahern. Die Ableitungsfunktion zu der in Abb. 8 dargestellten Funktion hat deshalb zwangslaufig die x-Achse 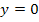als waagrechte Asymptote. Diese Bedingungen erfullt nur der in Abb. 11 gezeigte Graph. Deshalb kann nur Abb. 11 die Ableitungsfunktion zu der in Abb. 8 dargestellten Funktion zeigen.

Abb. 8

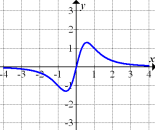
Abb. 11

Andere Paare aus Funktion und Ableitungsfunktion gibt es nicht.

---