a.) Unterschied zwischen Ableitung f´(x0) an einer bestimmten Stelle x0 und der Ableitungsfunktion f´(x)
Meist wird  einfach kurz als „Ableitung“ der Funktion
einfach kurz als „Ableitung“ der Funktion  bezeichnet, so auch oft auf dieser website. Streng genommen handelt es sich bei
bezeichnet, so auch oft auf dieser website. Streng genommen handelt es sich bei  aber um die sogenannte Ableitungsfunktion. Nicht nur
aber um die sogenannte Ableitungsfunktion. Nicht nur 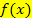 , sondern auch
, sondern auch 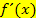 stellt eine eigene Funktion dar.
stellt eine eigene Funktion dar.
Beachte:Von der Ableitungsfunktion  ist die Ableitung
ist die Ableitung 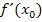 einer Funktion
einer Funktion  an einer bestimmten Stelle
an einer bestimmten Stelle 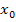 zu unterscheiden. (Mit
zu unterscheiden. (Mit 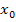 ist – im Gegensatz zu x – eine konkrete, feste Zahl gemeint. Achtung:x stellt eine Variable/veranderliche Zahl dar. Daher kann x verschiedene Werte annehmen, wogegen
ist – im Gegensatz zu x – eine konkrete, feste Zahl gemeint. Achtung:x stellt eine Variable/veranderliche Zahl dar. Daher kann x verschiedene Werte annehmen, wogegen 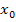 eine bestimmte, festgelegte Zahl ist.)
eine bestimmte, festgelegte Zahl ist.)
Mit 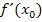 ist daher die Steigung einer Funktion
ist daher die Steigung einer Funktion  an einer bestimmten Stelle
an einer bestimmten Stelle 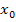 gemeint. Laut Definition gilt:Die Steigung einer Funktion
gemeint. Laut Definition gilt:Die Steigung einer Funktion  in einem festen Kurvenpunkt
in einem festen Kurvenpunkt 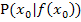 entspricht der Steigung der Tangente an den Graphen
entspricht der Steigung der Tangente an den Graphen 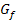 in diesem Punkt. Du kannst also den Begriff der Kurvensteigung immer mit dem der Tangentensteigung an dieser Stelle gleichsetzen. Somit ist
in diesem Punkt. Du kannst also den Begriff der Kurvensteigung immer mit dem der Tangentensteigung an dieser Stelle gleichsetzen. Somit ist 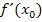 die Tangentensteigung der Funktion
die Tangentensteigung der Funktion  in diesem einen Kurvenpunkt
in diesem einen Kurvenpunkt 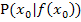 .
.
Daraus folgt: Die Ableitung in einem bestimmten Punkt 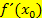 ist eine Zahl, welche die Tangentensteigung in diesem Punkt angibt, und nicht wie die Ableitungsfunktion
ist eine Zahl, welche die Tangentensteigung in diesem Punkt angibt, und nicht wie die Ableitungsfunktion 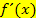 eine ganze Funktion!
eine ganze Funktion!
Unterscheide daher genau zwischen 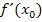 und
und  . Der erste Ausdruck
. Der erste Ausdruck 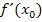 ist die Tangentensteigung im festen Kurvenpunkt
ist die Tangentensteigung im festen Kurvenpunkt 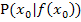 , der zweite Ausdruck
, der zweite Ausdruck  ist dagegen eine eigene Funktion, welche jedem x den Wert der Steigung der Funktion
ist dagegen eine eigene Funktion, welche jedem x den Wert der Steigung der Funktion  an dieser Stelle zuordnet. Die y-Koordinate eines Punktes auf der Ableitungsfunktion
an dieser Stelle zuordnet. Die y-Koordinate eines Punktes auf der Ableitungsfunktion  entspricht also immer der Steigung der Funktion
entspricht also immer der Steigung der Funktion  an der jeweiligen Stelle x.
an der jeweiligen Stelle x.
Konkretes Beispiel:
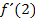 ist die Steigung der Tangente im Kurvenpunkt
ist die Steigung der Tangente im Kurvenpunkt 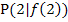 einer Funktion
einer Funktion  . In diesem Beispiel ist
. In diesem Beispiel ist 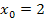 .
. 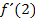 lasst sich ausrechnen, wenn man
lasst sich ausrechnen, wenn man  kennt, entweder umstandlich mit Hilfe des Differenzialquotienten oder mittels der Ableitungsregeln. (Siehe:Einfache Ableitungsregeln) Wir verwenden im Folgenden immer die Ableitungsregeln. Wenn du die Ableitungsregeln noch nicht gelernt hast oder in einer bestimmten Aufgabe nicht verwenden darfst, musst du die Ableitung leider mit dem Differenzialquotienten bilden. (Naheres unter:Herleitung der Tangentensteigung aus der Sekantensteigung mittels des Differenzialquotienten)
kennt, entweder umstandlich mit Hilfe des Differenzialquotienten oder mittels der Ableitungsregeln. (Siehe:Einfache Ableitungsregeln) Wir verwenden im Folgenden immer die Ableitungsregeln. Wenn du die Ableitungsregeln noch nicht gelernt hast oder in einer bestimmten Aufgabe nicht verwenden darfst, musst du die Ableitung leider mit dem Differenzialquotienten bilden. (Naheres unter:Herleitung der Tangentensteigung aus der Sekantensteigung mittels des Differenzialquotienten)
Nehmen wir als konkretes Beispiel die Funktion 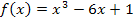 . Dann ist die Ableitungsfunktion
. Dann ist die Ableitungsfunktion 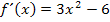 . Die y-Koordinaten der Ableitungsfunktion
. Die y-Koordinaten der Ableitungsfunktion 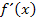 entsprechen dabei jeweils der Steigung der Funktion
entsprechen dabei jeweils der Steigung der Funktion  an der Stelle x. Die Steigung der Funktion an der Stelle
an der Stelle x. Die Steigung der Funktion an der Stelle 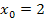 ist somit
ist somit 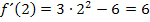 . Die Funktion
. Die Funktion  hat also an der Stelle
hat also an der Stelle 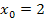 die Steigung 6. (Durch das Einsetzen der gegebenen x-Koordinate in die Ableitungsfunktion
die Steigung 6. (Durch das Einsetzen der gegebenen x-Koordinate in die Ableitungsfunktion 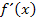 hat man also die Tangentensteigung von
hat man also die Tangentensteigung von  an dieser Stelle ausgerechnet.)
an dieser Stelle ausgerechnet.)
Die Ableitung 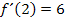 ist also eine konkrete Zahl, welche die Tangentensteigung an der festen Stelle
ist also eine konkrete Zahl, welche die Tangentensteigung an der festen Stelle 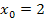 angibt. Im Gegensatz dazu ist
angibt. Im Gegensatz dazu ist 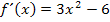 die Ableitungsfunktion.
die Ableitungsfunktion.  ist also eine richtige Funktion, wie auch
ist also eine richtige Funktion, wie auch  selbst. Die Ableitung
selbst. Die Ableitung  ist schlie?lich noch von x abhangig und stellt somit naturlich ebenfalls eine Funktion dar.
ist schlie?lich noch von x abhangig und stellt somit naturlich ebenfalls eine Funktion dar.

