Die Ableitungsfunktion f´(x)
Im Folgenden wird an sich vorausgesetzt, dass du einfache Funktionen mit Hilfe der einfacheren Ableitungsregeln bereits ableiten kannst, und dass du schon weißt, dass die Ableitung 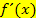 der Steigung einer Funktion
der Steigung einer Funktion 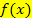 bzw. ihrer Tangentensteigung entspricht. Wenn dir der Begriff der Ableitung
bzw. ihrer Tangentensteigung entspricht. Wenn dir der Begriff der Ableitung  noch gar nichts sagt, solltest du unbedingt zuerst die Herleitung der Tangentensteigung aus der Sekantensteigung mittels des Differenzialquotienten durcharbeiten.
noch gar nichts sagt, solltest du unbedingt zuerst die Herleitung der Tangentensteigung aus der Sekantensteigung mittels des Differenzialquotienten durcharbeiten.
Hier trotzdem noch einmal eine ganz kurze Wiederholung der einfachen Ableitungsregeln:
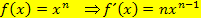
In Worten:Man leitet Funktionen der Form 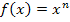 ab, indem man den Exponenten n nach vorne zieht und außerdem anschließend vom ursprünglichen Exponenten n die Zahl 1 abzieht.
ab, indem man den Exponenten n nach vorne zieht und außerdem anschließend vom ursprünglichen Exponenten n die Zahl 1 abzieht.
Bsp.: 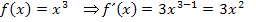
Wenn vor der x-Potenz noch ein Koeffizient (eine Zahl) steht, gilt:
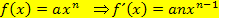
Der Koeffizient a ist eine Zahl, die multipliziert wird, eine sogenannte multiplikative Konstante. Solche Zahlen bleiben beim Ableiten quasi stehen. D.h. der Exponent wird mit a beim Ableiten multipliziert. Funktionen der Form 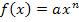 werden also abgeleitet, indem man den Exponenten n nach vorne zieht und mit dem Koeffizienten a multipliziert. Außerdem muss anschließend vom ursprünglichen Exponenten n die Zahl 1 abgezogen werden, das ergibt den Exponenten bei der Ableitung.
werden also abgeleitet, indem man den Exponenten n nach vorne zieht und mit dem Koeffizienten a multipliziert. Außerdem muss anschließend vom ursprünglichen Exponenten n die Zahl 1 abgezogen werden, das ergibt den Exponenten bei der Ableitung.
Bsp.: 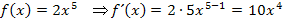
Zahlen ganz ohne x, die bei  addiert oder subtrahiert werden, fallen beim Ableiten komplett weg. (Multiplikative Konstanten, d.h. Zahlen ohne x mit mal oder geteilt, bleiben dagegen beim Ableiten stehen, z.B. Zahlen ohne x vor einer Klammer.) Bei Ausdrücken der Form „Zahl mal x“ fällt das x beim Ableiten weg, nur die Zahl bleibt stehen. So ergibt 5x abgeleitet einfach die Zahl 5. (Vergleiche nächstes Beispiel!) Mehrere Ausdrücke mit x, die bei
addiert oder subtrahiert werden, fallen beim Ableiten komplett weg. (Multiplikative Konstanten, d.h. Zahlen ohne x mit mal oder geteilt, bleiben dagegen beim Ableiten stehen, z.B. Zahlen ohne x vor einer Klammer.) Bei Ausdrücken der Form „Zahl mal x“ fällt das x beim Ableiten weg, nur die Zahl bleibt stehen. So ergibt 5x abgeleitet einfach die Zahl 5. (Vergleiche nächstes Beispiel!) Mehrere Ausdrücke mit x, die bei  addiert oder subtrahiert werden, dürfen einzeln nacheinander abgeleitet werden.
addiert oder subtrahiert werden, dürfen einzeln nacheinander abgeleitet werden.
Bsp.: 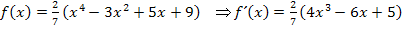
Aber Vorsicht bei Produkten, Quotienten und verketteten/verschachtelten Funktionen! Ein Produkt, das die Variable x in mehreren Faktoren enthält, muss zuerst ausmultipliziert werden, bevor du es mit den oben erwähnten Regeln ableiten kannst. (Ansonsten muss Die Produktregelangewendet werden.) Quotienten, die im Nenner die Variable x enthalten, musst du erst so umformen, dass kein x mehr im Nenner steht, bevor du nach den oben erwähnten Regeln ableiten darfst. (Lässt sich die Funktion nicht ohne x im Nenner schreiben, muss Die Quotientenregel angewendet werden.) Auch Funktionen, die ineinander verschachtelt sind, wie zum Beispiel 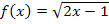 , können nicht so einfach abgeleitet werden. (Dazu braucht man Die Kettenregel.)
, können nicht so einfach abgeleitet werden. (Dazu braucht man Die Kettenregel.)
Soviel an dieser Stelle zu den Ableitungsregeln. Mehr dazu im Abschnitt:Einfache Ableitungsregeln
Zwei wichtige Punkte bezüglich  und
und  solltest du dir jetzt gleich bewusst machen:
solltest du dir jetzt gleich bewusst machen:
· Wenn du eine gegebene x-Koordinate eines Kurvenpunktes von  in die Funktionsgleichung
in die Funktionsgleichung  einsetzt, erhältst du die y-Koordinate dieses Kurvenpunktes;
einsetzt, erhältst du die y-Koordinate dieses Kurvenpunktes;  ist schließlich nur eine andere Schreibweise für y.
ist schließlich nur eine andere Schreibweise für y.
· Wenn du eine gegebene x-Koordinate eines Kurvenpunktes von 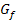 in die Ableitungsfunktion
in die Ableitungsfunktion 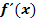 einsetzt, erhältst du die Steigung m des Graphen
einsetzt, erhältst du die Steigung m des Graphen 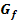 an dieser Stelle, d.h. die Steigung der Tangente im entsprechenden Kurvenpunkt;
an dieser Stelle, d.h. die Steigung der Tangente im entsprechenden Kurvenpunkt;  ist schließlich nur eine andere Schreibweise für die Tangentensteigung m.
ist schließlich nur eine andere Schreibweise für die Tangentensteigung m.
Merke:
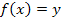
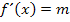 (Steigung von
(Steigung von 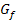 bzw. Tangentensteigung)
bzw. Tangentensteigung)
Um die y-Koordinate eines Punktes P der Funktion 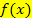 auszurechnen, setzt du die x-Koordinate von P immer in die Funktionsgleichung
auszurechnen, setzt du die x-Koordinate von P immer in die Funktionsgleichung 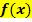 selbst ein und nicht in die Ableitungsfunktion
selbst ein und nicht in die Ableitungsfunktion 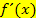 ! Um dagegen die Tangentensteigung von
! Um dagegen die Tangentensteigung von 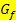 in einem bestimmten Punkt auszurechnen, setzt du die x-Koordinate des Punktes P immer in die Ableitung
in einem bestimmten Punkt auszurechnen, setzt du die x-Koordinate des Punktes P immer in die Ableitung 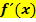 ein.
ein.
Der gegebene Kurvenpunkt hat dabei allgemein die x-Koordinate 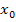 . Mit
. Mit 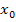 ist also immer die x-Koordinate eines Punktes auf der Funktion
ist also immer die x-Koordinate eines Punktes auf der Funktion  gemeint. Dabei stellt
gemeint. Dabei stellt 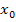 grundsätzlich eine konkrete, feste Zahl dar und keine Variable.
grundsätzlich eine konkrete, feste Zahl dar und keine Variable. 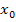 steht somit immer für eine bestimmte Zahl, wogegen x für die Variable steht.
steht somit immer für eine bestimmte Zahl, wogegen x für die Variable steht.
Auf den Unterschied zwischen 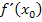 und
und  werden wir im folgenden Teil a.) näher eingehen. Zwischen
werden wir im folgenden Teil a.) näher eingehen. Zwischen 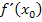 und
und  besteht nämlich ein großer Unterschied. Auch die Definition der Ableitungsfunktion findest du hier.
besteht nämlich ein großer Unterschied. Auch die Definition der Ableitungsfunktion findest du hier.
Im Teil b.) werden die wichtigsten Zusammenhänge zwischen Funktion  und zugehöriger Ableitungsfunktion
und zugehöriger Ableitungsfunktion  besprochen. Außerdem wird hier auch der Begriff der „Stammfunktion F“ eingeführt und die Zusammenhänge der Graphen einer Funktion f und ihrer Stammfunktion F erläutert. Zu all dem viele Beispielaufgaben, natürlich mit ausführlichen Lösungen.
besprochen. Außerdem wird hier auch der Begriff der „Stammfunktion F“ eingeführt und die Zusammenhänge der Graphen einer Funktion f und ihrer Stammfunktion F erläutert. Zu all dem viele Beispielaufgaben, natürlich mit ausführlichen Lösungen.
| a.) Unterschied zwischen Ableitung f´(x0) an einer bestimmten Stelle x0 und der Ableitungsfunktion f´(x)
b.) Zusammenhang der Funktion f (x) mit ihrer Ableitungsfunktion f´(x) |

