Das Newton-Verfahren
Wofür braucht man das Newton-Verfahren?
Das Newton-Verfahren ist eine Methode, mit der du alle Gleichungen, die sich algebraisch nicht nach x auflösen lassen, zumindest ungefähr (näherungsweise) lösen kannst. Das Newton-Verfahren geht, wie schon der Name verrät, auf den englischen Mathematiker und Physiker Sir Isaac Newton (1643 – 1727) zurück. Es handelt sich bei diesem Verfahren um ein sogenanntes Iterationsverfahren, d.h. ein Lösungsverfahren, bei dem eine bestimmte Rechenoperation immer wieder in gleicher Art und Weise vollzogen wird, und das so Schritt für Schritt immer genauere Näherungswerte für die gesuchte Lösung x liefert. Aus der 9. Klasse kennst du vermutlich schon das Heron-Verfahren zur näherungsweisen Berechnung von Quadratwurzeln. Auch das Heron-Verfahren ist ein Iterationsverfahren. (Genau genommen stellt es einen Sonderfall des Newton-Verfahrens dar.) Bei einem solchen Verfahren gibt eine sogenannte Iterationsvorschrift (Rechenanweisung) an, welche Rechenoperationen immer wieder nacheinander vollzogen werden müssen, bis die gewünschte Genauigkeit der Lösung erreicht ist. (In vielen Aufgaben ist bereits vorgegeben, auf wie viele Dezimalen genau das Ergebnis angegeben werden soll. Z.B.:Ermittle die Lösung auf 2 Dezimalen! Dann sollst du das Ergebnis natürlich auf zwei Nachkommastellen gerundet berechnen.) Wie diese Iterationsvorschrift beim Newton-Verfahren aussieht und wie man sie verwendet, wird weiter unten erklärt. Je öfter du die Iterationsvorschrift anwendest, desto genauer wird das Ergebnis.
Du erhältst also durch das Newton-Verfahren nicht die exakte Lösung einer Gleichung, bloßeinen beliebig genauen Näherungswert.
Wie genau dieser Wert ist, hängt davon ab, wie oft du die Iterationsvorschrift (Rechenanweisung) benutzt hast, also wie viel Rechenarbeit du investiert hast. Wie schnell sich die Lösung mit der gewünschten Genauigkeit ergibt, hängt vor allem von der Wahl eines guten Startwertes 
ab. Was dieser Startwert ist und wie man einen geeigneten Wert finden kann, falls er in der Aufgabenstellung nicht schon gegeben ist, werden wir weiter unten noch genau besprechen.
Du kannst das Newton-Verfahren auf jeden Fall immer dann anwenden, wenn du eine Gleichung nach x auflösen willst, dies aber mit den „normalen“ Methoden, wie Äquivalenzumformungen, Mitternachtsformel oder Erraten einer Lösung und darauf folgende Polynomdivision, nicht klappt.
Vielleicht hast du dich schon einmal gefragt, was man denn macht, wenn sich zum Beispiel bei einer Gleichung der Form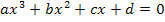 
absolut keine Lösung erraten lässt. Dann kann man ja keine Polynomdivision machen, weil man nicht weiß, wodurch man überhaupt dividieren soll. An Stelle der Polynomdivision könntest du dann das Newton-Verfahren einsetzen. Das gleiche gilt bei allen anderen schwierigen Gleichungen, wie beispielsweise 
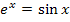. So eine Gleichung kann nicht auf „normalem“ Weg nach x aufgelöst werden;man benötigt ein Näherungsverfahren. Es gibt diverse graphische und rechnerische Näherungsverfahren, doch wollen wir uns an dieser Stelle ausschließlich mit dem Newton-Verfahren beschäftigen.
