Aufgaben mit Funktionenscharen, Ortskurven von Hoch-, Tief- oder Wendepunkten berechnen
Enthält eine gegebene Funktionsgleichung neben der Variablen einen oder mehrere weitere Buchstaben wie zum Beispiel a oder k liegt eine Funktionenschar vor. Eine Schar von Funktionen besteht praktisch aus vielen verschiedenen einzelnen Funktionen.
Beispiel einer Funktionenschar: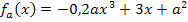 
Der Buchstabe, der hinter f in der Klammer steht, ist die Variable. Der Buchstabe a ist hier der sogenannte Scharparameter, kurz Parameter. Am Auftreten eines Parameters (oder mehrerer Parameter) in der Funktionsgleichung erkennst du, dass eine Funktionenschar vorliegt. Ein Parameter stellt grundsätzlich eine konkrete, feste Zahl dar, auch wenn man diese Zahl nicht kennt. Oft (aber nicht immer) steht derjenige Buchstabe, der den Parameter darstellt, bei der Funktionsbezeichnung als Index angegeben, d.h. als kleiner geschriebener, tiefergestellter Buchstabe.
Bei 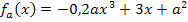ist a der Parameter und x die Variable.
Nur wenn man weiß, welchen Wert der Parameter a hat, kann man den Graph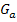 
dieser einen Funktion der Schar zeichnen. Solange nichts anderes angegeben ist, kann a für eine beliebige reelle Zahl stehen, d.h. es gilt a 
ℝ, so dass es eigentlich unendlich viele verschiedene Funktionen gibt, die alle zu der Schar gehören. Man kann natürlich nicht unendlich viele verschiedene Graphen zeichnen. Deshalb kann man niemals die gesamte Schar zeichnen, sondern immer nur die Graphen von einzelnen Funktionen, die zu der jeweiligen Schar gehören. (Meistens werden maximal drei, selten bis zu sechs verschiedene Werte für den Parameter angegeben. Für diese Werte sollen dann die einzelnen Graphen der Schar gezeichnet werden.)
Soll beispielsweise der Graph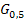 
(d.h. der Graph für a = 0,5) gezeichnet werden, setzt man für a die Zahl 0,5 in die Gleichung der Schar 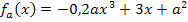ein. So kommt man auf die Gleichung 
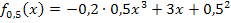bzw. vereinfacht zu 
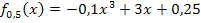. Nun kann der zugehörige Graph 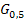mit einer Wertetabelle leicht gezeichnet werden.
Leider ist aber der Parameter nicht immer gleich direkt angegeben. Bei manchen Aufgaben musst du den Parameter vorab erst selbst berechnen, zum Beispiel so, dass ein gegebener Punkt auf dem Graphen liegt, oder dass der einzige Kurvenpunkt mit waagrechter Tangente eine bestimmte x-Koordinate hat. In anderen Aufgaben soll der Parameter so berechnet werden, dass die Funktion an einer bestimmten Stelle eine ganz bestimmte Steigung hat. Wie das funktioniert, werden wir uns gleich an einigen konkreten Beispielen anschauen.
1. Bsp.:
Wir betrachten die Funktionenschar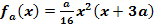 
mit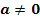 
. Die Graphen der Schar werden mit 
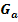bezeichnet.
a.) Für welche Werte von a liegt der Punkt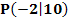 
auf ?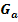
b.) Welche Funktion der Schar hat bei x = 4 eine waagrechte Tangente?
c.) Für welche Werte von a verläuft die Tangente an 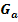im Punkt 
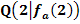parallel zu der Geraden 
?
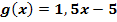Lösung:
Zu 1a.)
Geg.: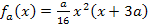 
mit 
Es sollen diejenigen Werte von a berechnet werden, für die der Punkt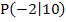 
auf dem Graph 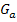liegt.
