Einführung in die Differenzialrechnung
Die Differenzialrechnung stellt ein wichtiges Teilgebiet der Analysis dar. Es geht dabei um Berechnungen mit Funktionen und ihren Ableitungen. Die erste Ableitung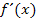 
einer Funktion 
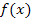ist nichts anderes als die Steigung der Funktion. Das Berechnen von 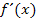nennt man „ableiten“ oder auch „differenzieren“. Daher die Bezeichnung Differenzialrechnung. Die Anwendungen der Differenzialrechnung sind vielfältig.
Hier eine Übersicht in Stichpunkten über den Lehrstoff dieses Kapitels:
Und hier noch eine ausführlichere Komplettübersicht über den gesamten behandelten Stoff dieses Kapitels mit Anmerkungen, für welche Schüler dieser Stoff relevant ist, und zur Erklärung der einzelnen Punkte die jeweils typischen Fragestellungen dazu:
| · Für Schüler einer 11. Klasse Gymnasium und 12. Klasse FOS/BOS: Was ist „Differenzialrechnung“ überhaupt und was kann damit berechnet werden? Wie ist die Steigung einer beliebigen Funktion definiert und was versteht man unter dem Begriff der „Ableitung“ einer Funktion? Ein kurzes Vorwort zur Differenzialrechnung
· Für alle Schüler einer 11. Klasse G8 und 12. Klasse FOS/BOS: Wie kommt man von der Sekantensteigung zur Tangentensteigung? Was versteht man unter den Begriffen „Differenzenquotient“ und „Differenzialquotient“ und was ist die erste Ableitung Es gibt dabei jeweils drei verschiedene Ansätze für den Differenzen- und den Differenzialquotienten. Je nachdem, wie ihr es im Schulunterricht gemacht habt, wählst du die für dich passende Variante: Delta-x-Methode,mit Die h-Methode,mit Variante 3,mit Für Schüler, die mehrere Ansätze des Differenzialquotienten gelernt haben: Welchen Ansatz bei welchen Aufgaben verwenden Außerdem wird speziell für G8 Schüler gegen Ende des Abschnitts genau erläutert, was die Begriffe „mittlere Änderungsrate“ und „lokale Änderungsrate“ mit den Begriffen „Differenzenquotient“ und „Differenzialquotient“ zu tun haben. · Für alle Schüler ab 11. Klasse G8 und 12. Klasse FOS/BOS super wichtig, weil Grundlage für alles weitere: Wie bildet man die Ableitung · Für alle Schüler ab 11. Klasse G8 und 12. Klasse FOS/BOS sehr wichtig: Wie hängt der Graph einer Funktion · Nur für Schüler eines Gymnasiums (G8) ab der 11. Klasse oder einer 12. Klasse FOS/BOS mathematischer Zweig:Mit Hilfe der ersten Ableitung lässt sich ein Verfahren zur näherungsweisen Berechnung der Nullstellen schwieriger Funktionen entwickeln. Wie sich z.B. die Nullstellen eines Polynoms dritten oder höheren Grades zumindest näherungsweise berechnen lassen, auch wenn keine Nullstelle erraten werden kann und daher keine Polynomdivision möglich ist, wird vorgeführt im Teil: Das Newton-Verfahren · Nur für Schüler ab 11. Klasse G8 und 12. Klasse FOS/BOS mathematisch/technischer Zweig: Wie lassen sich auch schwierigere Funktionen mit Hilfe der Produkt-, Quotienten- und Kettenregel ableiten? Wie bildet man die Ableitungen der Exponentialfunktion Dieser Teil besteht aus den folgenden Punkten:
· Für alle Schüler ab 11. Klasse G8 und 12. Klasse FOS/BOS: Was ist, wenn der Graph einer Funktion an einer bestimmten Stelle einen Sprung macht oder einen Knick hat? Dann kann man an dieser Stelle die Steigung der Funktion nicht angegeben. Wie zeigt man dann durch Rechnung, dass bei dieser Funktion eine Sprungstelle oder ein Knick vorliegt? Wie ermittelt man den Knickwinkel sowie ein Extremum an einer Knickstelle? Das alles wird erläutert im Teil: Stetigkeit und Differenzierbarkeit · Für alle Schüler einer 12. Klasse G8 oder FOS/BOS: Was bedeutet die zweite Ableitung anschaulich? Was versteht man unter einem Wendepunkt; wie wird er berechnet und mit Hilfe des Krümmungsverhaltens der Funktion nachgewiesen? Wie wird die Krümmung einer Funktion rechnerisch untersucht, d.h. wie fertigt man eine Krümmungstabelle an? Wie ermittelt man die Gleichung einer Wendetangente und wie findet man die Art der Extrema mit der zweiten Ableitung heraus? Alle diese Fragen werden beantwortet im Teil:Zweite Ableitung f´´(x) · Nur für Schüler, welche die dritte Ableitung · Für alle Schüler einer 11. Klasse G8 und 12. Klasse FOS/BOS sehr wichtig, aber schwierig: Eine zylindrischen Dose soll ein Volumen von 0,33 l haben. Wie müssen Radius und Höhe der Dose gewählt werden, damit Ihre Oberfläche und somit auch der Materialverbrauch minimal wird? Wie man Aufgaben dieses Typs lösen kann, wird erklärt im Teil:Extremwertaufgaben mit Nebenbedingung / Optimierungsprobleme · Für alle Schüler ab 11. Klasse:Wenn von einer Funktion einige bestimmte Eigenschaften, wie zum Beispiel eine Nullstelle und ein Hochpunkt/ Tiefpunkt oder ein Wendepunkt gegeben sind:Wie findet man dann die Funktionsgleichung? Das wird erklärt im Teil: Funktionsgleichungen mit gegebenen Eigenschaften aufstellen und Funktionen modellieren · Für alle Schüler ab 11. Klasse: Kommt in einer Funktionsgleichung neben der Variablen x ein weiterer Buchstabe z. B. a oder k vor, so liegt eine Funktionenschar vor. Solche Aufgaben stellen besonders hohe Anforderungen an deine mathematischen Fähigkeiten, sind aber extrem wichtig. Wie man zum Beispiel die Gleichung einer Kurve ausrechnet, auf der alle Hoch- oder Tiefpunkte einer bestimmten Schar liegen, und andere typischen Aufgaben rund um das Thema Funktionenscharen werden erklärt bei: Aufgaben mit Funktionenscharen, Ortskurven von Hoch-, Tief- oder Wendepunkten berechnen |
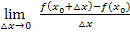
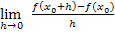
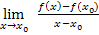
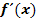einer Funktion? Wie funktioniert die h-Methode? All das wird erklärt im Teil: 
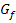? Was ist überhaupt eine Normale? Wie ermittelt man das Monotonieverhalten einer Funktion, d.h. in welchen Bereichen steigt oder fällt der Graph, und wie berechnet man Extrema? Was ist eine Stammfunktion F(x)? All diese Fragen werden ausführlich besprochen im Teil: 
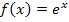sowie die Ableitungen der trigonometrischen Funktionen 
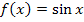und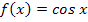 
? Das wird an Hand vieler Beispiele erklärt im Teil: 
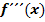im Unterricht behandelt haben: Was bedeutet die dritte Ableitung anschaulich? Wie kann man einen Wendepunkt auch mit der dritten Ableitung nachweisen? Dies wird besprochen im Teil:
