Grenzwerte von e- und ln-Funktionen

Damit du schwierigere Grenzwerte von e- bzw. ln-Funktionen ermitteln kannst, musst du unbedingt die folgenden Grenzwerte kennen:

a.) Grenzwerte der e-Funktion 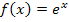mit :

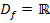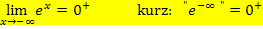
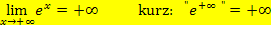
Wichtig: 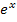wächst schneller als jede Potenz- oder Polynomfunktion!

b.) Grenzwerte der ln-Funktion 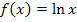mit

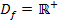
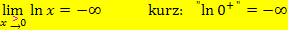
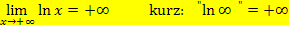
Wichtig: 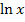wächst langsamer als jede Potenz- oder Polynomfunktion und natürlich auch langsamer als !

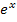Hinweis:

Alles, was in diesem Teil in Anführungsstriche gesetzt geschrieben ist, ist an sich nicht ganz mathematisch korrekt. Du solltest das in Prüfungen nicht so schreiben. Diese Schreibweise wurde nur gewählt, damit du dir die genannten Grenzwerte besser merken kannst.

Außerdem werden im Folgenden oft Zwischenüberlegungen bei komplizierteren Grenzwerten ebenfalls mit Anführungsstrichen geschrieben. Auch das ist an sich nicht mathematisch korrekt. Die Ausdrücke, die bei den folgenden Grenzwertberechnungen in Anführungsstriche geschrieben sind, stellen bloßÜberlegungen dar, die eigentlich im Kopf gemacht und nicht hingeschrieben werden sollen. Sie sind auf dieser website nur aufgeschrieben, damit du die jeweilige Berechnung des Grenzwertes besser nachvollziehen kannst. Du solltest die  mit Anführungsstrichen versehenen Zwischenschritte bei Prüfungen lieber nicht auf dein Blatt schreiben.

Nun schauen wir uns gleich ein paar Aufgabenbeispiele an. Im 1. Bsp. geht es ausnahmslos um einfachere Grenzwerte. Sie dienen eher der Vorübung für die schwierigeren nachfolgenden Aufgaben. Alle Teilaufgaben des ersten Beispiels solltest du im Prinzip im Kopf lösen können. Versuche es doch gleich selbst!

1. Bsp.:

Ermittle die Ergebnisse folgender Grenzwerte!

a.)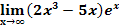

b.)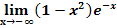

c.)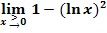

d.)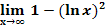

e.)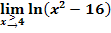

f.)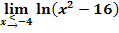

g.)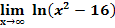

h.)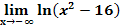

Lösung:

Ein kleiner Tipp vorweg:Bei einem Polynom brauchst du immer nur die höchste x-Potenz und die Zahl davor beachten, wenn du den Grenzwert im Unendlichen berechnest. Du musst Unendlich bzw. Minus-Unendlich bloßbei dem x mit der höchsten Potenz einsetzen und dir vor allem das entstehende Vorzeichen überlegen. Nur die höchste x-Potenz mit der Zahl davor zählt! Alle anderen Zahlen und Potenzen von x kannst du vernachlässigen, da sie im Unendlichen gegenüber der höchsten x-Potenz kaum ins Gewicht fallen.

Zu 1a.)

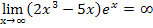
Wie kommt man auf dieses Ergebnis? Weil es sich bei der Funktion 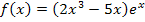um ein Produkt handelt, überlegt man sich den Grenzwert bei jedem Faktor des Produkts einzeln und multipliziert anschließend die einzelnen Ergebnisse. Du musst dich also zuerst fragen, wohin geht 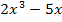für 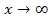und wohin geht 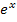für .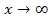

Der erste Faktor 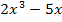ist ein Polynom, daher setzen wir (in Gedanken) Unendlich nur in die höchste x-Potenz ein, um das Verhalten dieses Faktors im Unendlichen zu ermitteln. Wir ignorieren also den Term -5x bei der Berechnung des Grenzwertes und setzen Unendlich nur bei 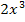ein. Wegen 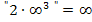geht der erste Faktor gegen Unendlich.

Der zweite Faktor ist 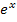, was bekanntlich für ebenfalls gegen Unendlich geht. Es gilt schließlich: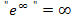

Beide Faktoren gehen also jeweils gegen Unendlich. Unendlich mal Unendlich ist natürlich wieder Unendlich. (Eine unendlich große Zahl mit einer anderen unendlich großen Zahl multipliziert, wird schließlich wieder unendlich groß.) Deshalb kommt insgesamt Unendlich heraus.

---