Definitionsmenge ermitteln bei e- und ln- Funktionen
Die Definitionsmenge 
einer Funktion 
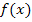enthält alle die Zahlen, welche bei 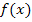für x eingesetzt werden dürfen. Die maximale Definitionsmenge einer Funktion 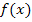ist, wie der Name schon sagt, die größtmögliche Definitionsmenge dieser Funktion. Ist in einer Aufgabe nach der Definitionsmenge einer Funktion 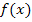gefragt, ist grundsätzlich die maximale Definitionsmenge gemeint. Du musst dann die Menge aller Zahlen ermitteln, die in 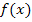überhaupt für x eingesetzt werden dürfen.
Wenn du die maximale Definitionsmenge einer e- oder ln-Funktion ermitteln sollst, musst du folgende Aspekte beachten:
- Falls ein ln vorkommt:
Das Argument des ln (d.h. der Ausdruck, auf den sich der ln bezieht;also die Klammer, die direkt hinter ln steht) muss positiv sein. (lnx ist nämlich nur für x >0 definiert.)
Die Klammer, die direkt hinter ln steht >0 setzen und die Ungleichung nach x auflösen;das ergibt die Definitionsmenge, falls nicht noch ein weiterer Aspekt beachtet werden muss.
- Falls ein Bruch vorliegt, der die Variable im Nenner enthält:Der Nenner darf nicht gleich Null sein. (Die Division durch Null ist bekanntlich nicht definiert.)
Nenner gleich Null setzen und nach x auflösen;das Ergebnis aus der Definitionsmenge ausschließen
- Falls eine Wurzel vorkommt, deren Radikand (= Ausdruck unter der Wurzel) die Variable enthält:Der Radikand darf nicht negativ sein, muss also größer oder gleich Null sein. (
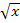ist nämlich ausschließlich für 
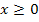definiert.)
Den Ausdruck unter der Wurzel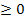 
setzen und die Ungleichung nach x auflösen;das ergibt die Definitionsmenge, falls nicht noch ein weiterer Aspekt beachtet werden muss.
Bei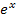 
kann man alle reellen Zahlen für x einsetzen, weil 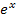für x 
ℝ definiert ist. Daher brauchst du bei Ausdrücken der Form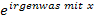 
gar nichts Besonderes beachten. Wenn kein anderer der oben genannten Aspekte zu beachten ist, gilt für die maximale Definitionsmenge der Funktion 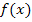automatisch: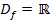 
Die Frage nach der größtmöglichen Definitionsmenge einer Funktion kommt wirklich sehr oft in Prüfungen vor. Jede Kurvendiskussion beginnt schließlich mit der Ermittlung der Definitionsmenge, außer sie ist bereits angegeben. Vor allem bei Funktionen mit ln ist es leider oft gar nicht so einfach, die Definitionsmenge zu finden. Das liegt an den Ungleichungen, die dabei zu lösen sind.
Du musst das aber wirklich gut können, denn es gibt nichts Schlimmeres als eine falsche Definitionsmenge!
Ist in einer Aufgabe zum Beispiel das Verhalten an den Rändern der Definitionsmenge zu untersuchen, würdest du völlig falsche Grenzwerte berechnen, wenn du von einer falschen Definitionsmenge ausgehst.
Deshalb üben wir das Ganze gleich an vielen, konkreten Aufgabenbeispielen. Los geht´s im 1. Bsp. mit verschiedenen e-Funktionen. Da ist es meistens noch ganz einfach die Definitionsmenge anzugeben. Im 2. Bsp. wird dann die Definitionsmenge der deutlich schwierigeren ln-Funktionen behandelt.
