Gleichungen mit lnx oder e^x lösen, einschließlich ln-Rechengesetze

Wann musst du den ln anwenden?

Den ln brauchst du immer, wenn du bei einer Gleichung der Form 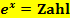nach x auflösen willst. Der ln holt bei 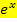praktisch das x aus dem Exponenten herunter.

Bsp.:

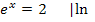
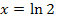
Man könnte das Ergebnis ln2 noch gerundet angeben, aber exakt lässt sich ln2 nicht als Dezimalzahl oder Bruch angeben. Ln2 ist eine irrationale Zahl, d.h. eine Zahl mit unendlich vielen, nicht periodischen Nachkommastellen:ln2 ℝ , aber ln2 ℚ.

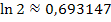
Meistens lässt man so ein Ergebnis wie ln2 jedoch einfach stehen und rundet es nicht. (Das ist so ähnlich wie bei 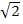: Das rechnet man schließlich auch in der Regel gar nicht mit dem Taschenrechner aus, sondern man lässt 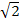einfach stehen, außer es ist ein gerundetes Ergebnis verlangt.)

Manchmal erhält man vor allem bei der Berechnung von bestimmten Integralen (erst Stoff 12. Klasse) Ergebnisse wie zum Beispiel ln2 + 3ln4 – ln8. Das solltest du dann auch nicht gleich in den Taschenrechner eingeben, sondern erst einmal mit den Logarithmus-Rechengesetzen soweit möglich vereinfachen. Sonst gibt es in Prüfungen nämlich Punktabzug!

Allgemein gilt:Wenn man noch etwas rechnen kann, sollte man es auch auf jeden Fall tun! Bei ln2 + 3ln4 – ln8 lässt sich beispielsweise noch eine Menge machen! Was man da noch rechnen kann? Überlege doch mal selbst!

Die Logarithmus-Rechengesetze gelten für Logarithmen zur allgemeinen Basis a mit (a >0 und 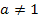), also natürlich auch für den Logarithmus zur Basis e , den ln.

Hier noch einmal die Logarithmus-Rechengesetze, aber jetzt speziell für den natürlichen Logarithmus ln:

ln-Rechengesetze:

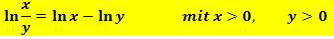
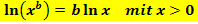
Wie lässt sich nun der oben erwähnte Ausdruck ln2 + 3ln4 – ln8 weiter vereinfachen? Vorab schreiben wir die Zahl 4 und die Zahl 8 als Zweierpotenz.

Bekanntlich gilt: 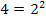und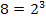

Damit ergibt sich:

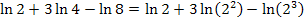
Nun lässt sich das dritte ln-Rechengesetz anwenden:

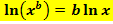
Wir ziehen also die Exponenten jeweils vor den zugehörigen ln.

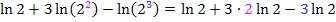
Ab jetzt ist es nicht mehr schwer. Man kann ganz leicht zusammenfassen, weil sich „zufälligerweise“ nur Vielfache von ln2 ergeben haben.

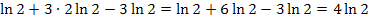
So würde man das Ergebnis nun wirklich stehen lassen;d.h. 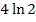wäre dann das Endergebnis und nicht 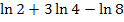(das wäre nur Zwischenergebnis.).

Auch Ausdrücke wie zum Beispiel ln0,5 oder 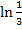solltest du so nicht als Endergebnis stehen lassen, sondern besser folgendermaßen umformen:

Vereinfachung von ln0,5:

Mit dem zweiten ln-Rechengesetz: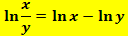

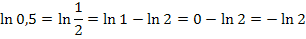
Hinweis: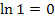

Oder alternativ dazu mit dem dritten ln-Rechengesetz: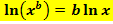

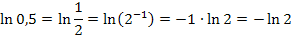
Vereinfachung von :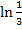

Mit dem zweiten ln-Rechengesetz:

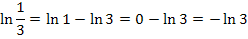
Oder alternativ dazu mit dem dritten ln-Rechengesetz:

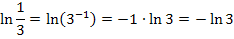
Allgemein gilt entsprechend:

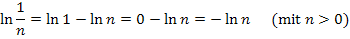
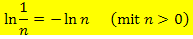
Mit Hilfe der ln-Rechengesetze lassen sich auch ln-Funktionen vereinfachen. Dabei musst du aber sehr aufpassen, denn es kann sich durch die Anwendung eines ln-Rechengesetzes die Definitionsmenge der Funktion verändern. In diesem Fall musst du von der Anwendung der ln-Rechengesetze absehen, denn du verlierst dann eventuell eine oder mehrere Lösungen z.B. bei der Berechnung der Extrema einer Funktion!

---