Satz von Vieta
In diesem Kapitel wird vorausgesetzt, dass du weißt, was eine (gemischt)quadratische Gleichung ist, was man unter der normierten Form einer quadratischen Gleichung versteht, und wie man mit der Mitternachtsformel generell gemischtquadratische Gleichungen löst. Falls du erst Erklärungen zu diesen Fragen benötigst, gehe vorher zu den Kapiteln Einführung in die quadratischen Gleichungen und Mitternachtsformel.
Vieta ist die latinisierte Form von Viète. Der Satz von Vieta ist nämlich benannt nach dem französischen Mathematiker François Viète (1540 – 1603). Ihm ist folgender Zusammenhang der beiden Lösungen 
und 
mit den Koeffizienten p und q einer normierten quadratischen Gleichung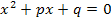 
aufgefallen:Multipliziert man die beiden Lösungen 
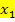und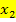 
miteinander, so ergibt sich genau der Koeffizient q. Addiert man die beiden Lösungen 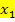und 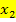, erhält man -p (also p aber mit umgedrehtem Vorzeichen). Machen wir uns diesen Zusammenhang der beiden Lösungen und mit den Koeffizienten p und q an einem konkreten Beispiel klar:
1. Bsp.:
Berechne zuerst die Lösungen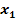 
und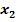 
der Gleichung 
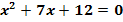und überprüfe dann durch Rechnung die Richtigkeit der Aussagen 
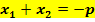und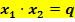 
!
Lösung:
Gegeben ist die gemischtquadratische Gleichung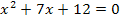 
. Mit der Mitternachtsformel lassen sich leicht die beiden Lösungen und berechnen. Rechne sie doch gleich ´mal selbst aus! Sie lauten:
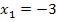und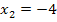 
Zur Kontrolle (oder Korrektur) deiner Rechnung:Hier nachträglich der komplette Rechenweg zur Gleichung
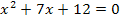
Vermutlich bist du es eher gewohnt mit der allgemeinen quadratischen Gleichung in der Form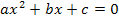 
zu arbeiten und nicht mit der normierten Form 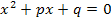. Deshalb bleiben wir zuerst noch bei den Bezeichnungen a, b und c. Damit du leichter erkennen kannst, was hier den Koeffizienten a, b und c der Mitternachtsformel entspricht, das Ganze noch einmal in verschiedenen Farben dargestellt:
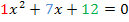
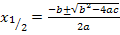
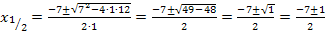
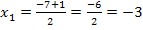
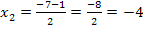
So, wir kennen also die beiden Lösungen 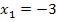und 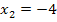unserer quadratischen Gleichung .
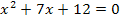