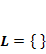Rechnerische Lösungsverfahren quadratischer Gleichungen

Für die rechnerische Lösung quadratischer Gleichungen wird die Kenntnis der Quadratwurzel vorausgesetzt. Wenn du dich nicht mehr sicher fühlst im Umgang mit der Wurzel, wiederhole zuerst kurz dieses Thema! Mehr zur Wurzel und zum Wurzelziehen findest du im Kapitel:Die Quadratwurzel und das Wurzelziehen (= Radizieren)

Wir beginnen mit dem einfachsten Typ, den reinquadratischen Gleichungen, also Gleichungen, welche zwar 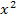und eine Konstante (= Zahl), aber kein x (ohne Potenz) enthalten. Vermutlich hast du bereits beim Rechnen mit Quadratwurzeln gelernt, diese Gleichungen zu lösen. Es dürfte daher eine Wiederholung für dich sein. Schau dir die folgenden Beispiele trotzdem kurz an!

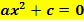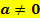Typ I mit (Wiederholung der reinquadratischen Gleichungen)

Anleitung zur Lösung reinquadratischer Gleichungen:Forme die Gleichung so um, dass 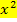alleine auf einer Seite der Gleichung steht ( 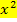isolieren) und ziehe dann die Wurzel.

Vorsicht:Aus einer negativen Zahl kann man keine Wurzel ziehen! Dann ist die Lösungsmenge einfach leer. Vergiss außerdem nicht das 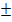vor der Wurzel, falls der Radikand (=Zahl unter der Wurzel) positiv ist!

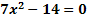
1. Bsp.: G = ℝ

Lösung:

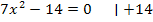
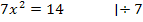
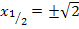
Oder ausführlich:  ;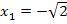 

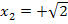
Warum muss das 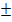Zeichen vor die Wurzel gesetzt werden? Da 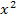einen geraden Exponenten hat, gibt es zwei verschiedene Lösungen, eine positive und eine negative. Egal ob man 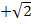oder 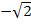für x einsetzt, ergibt sich nach dem Quadrieren jedes Mal als Ergebnis die Zahl 2. Die beiden Zahlen 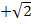und 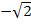sind irrationale Zahlen. Die Grundmenge ist laut Angabe G = ℝ, also die Menge der reellen Zahlen, zu der bekanntlich auch die irrationalen Zahlen gehören. Die Zahlen 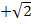und 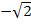sind deshalb in der Grundmenge enthalten. Die Lösungsmenge lautet daher:

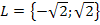
Anmerkung:Mit der Grundmenge G = ℚ wäre die Gleichung nicht lösbar gewesen, da die Zahlen 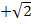und 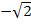nicht zur Menge ℚ, der Menge der rationalen Zahlen,gehören. Die Zahlen 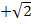und 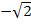sind schließlich irrational. In der Menge ℚ wäre die Lösungsmenge L leer.

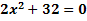
2. Bsp.: G=ℝ

Lösung:

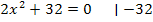
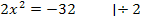
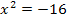
Vorsicht:Aus einer negativen Zahl kann man keine Wurzel ziehen!

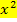kann gar nicht negativ werden und deshalb gibt es keine reelle Zahl, die die Gleichung erfüllt!

Nun kommt ein neuer Typ. Er stellt einen Sonderfall der gemischtquadratischen Gleichung dar, weil er zwar ein 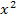und ein x (ohne Quadrat), aber keine Zahl ohne x enthält.

Typ II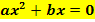

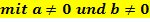
Enthält eine Gleichung ein 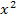und ein x (ohne Potenz), aber keine Konstante (= Zahl ohne x). lässt sie sich ganz schnell lösen. Hier hilft es allerdings nicht, 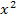zu isolieren. Im Gegenteil:Es muss in diesem Fall, wie auch bei schwierigeren gemischtquadratischen Gleichungen, alles auf einer Seite der Gleichung stehen, also keinesfalls 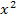auf die eine und x auf die andere Seite der Gleichung bringen. Wie sich dieser Typ dann lösen lässt, zeigt dir die folgende Anleitung:

Anleitung:Klammere zuerst x aus und setze dann die einzelnen Faktoren des entstehenden Produkts, also x und die Klammer, einzeln gleich Null! Wenn es möglich ist, kannst du natürlich zusätzlich zu x auch noch eine Zahl ausklammern. (Vergleiche 4.Bsp.!)

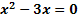
3. Bsp.: G=ℝ

Lösung:

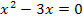
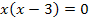
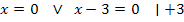
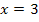
Erläuterung:Ein Produkt ist gleich Null, wenn einer der Faktoren gleich Null ist. Daher darf man die Faktoren einzeln gleich Null setzen. Die Gleichung ist deshalb durch die beiden Zahlen 0 und 3 erfüllt.

---