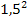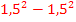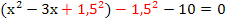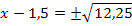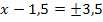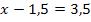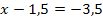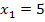Quadratische Ergänzung (zur Lösung gemischtquadratischer Gleichungen)
Im Folgenden wird gezeigt, wie man mit der sogenannten quadratischen Ergänzung gemischtquadratische Gleichungen, also Gleichungen vom Typ 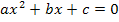 nach x auflösen kann.
nach x auflösen kann.
Da dieses Verfahren nicht so ganz einfach ist, wird parallel zur Anleitung sofort ein Beispiel gezeigt. So kannst du Schritt für Schritt sehen, wie es funktioniert. Es gibt allerdings zwei verschiedene Varianten der quadratischen Ergänzung zur Lösung von gemischtquadratischen Gleichungen. Sie dauern beide gleich lang und führen immer beide zum gewünschten Ergebnis. Manche Lehrer verwenden immer die erste, andere Lehrer die zweite Variante. Schau´einfach in dein Schulheft, wie es dein Lehrer macht! Ergänzt er nur auf einer Seite der Gleichung und macht zuerst + dann wieder – einen bestimmten Ausdruck (Erklärung folgt noch), wählst du die 1. Variante! Ergänzt er auf beiden Seiten der Gleichung mit dem selben Ausdruck, verwendest du die 2. Variante! Sollte dir jetzt noch nicht klar sein, welche Variante du brauchst, vergleiche das in der Tabelle rechts gezeigte Beispiel mit einer Aufgabe, die du im Schulheft hast! So müsstest du herausfinden können, welche Variante dein Lehrer in der Schule verwendet. Nur diese musst du dann lernen.
Geg.: 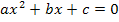 |
Geg.: 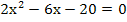 |
| Anleitung zur quadratischen Ergänzung
1. Variante |
Konkretes Beispiel |
| 1. Schritt:a ausklammern
d.h. jeden Faktor einzeln durch a teilen |
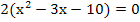 |
| 2. Schritt: Durch a auf beiden Seiten der Gleichung teilen | 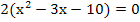 | | 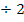
|
| 3. Schritt:Quadratisch ergänzen, um eine binomische Formel herzustellen
d.h. man nimmt die Zahl vor dem x (ohne Vorzeichen) halbiert und quadriert sie;das addiert man zuerst und subtrahiert dann gleich wieder, damit sich an der Gleichung insgesamt nichts ändert. (Man muss immer zuerst + und erst danach – schreiben, da andernfalls keine binomische Formel entsteht. Weder die erste noch die zweite binomische Formel haben hinten ein Minus!) Zur Wiederholung: 1. Binom: 2. Binom: |
Die Zahl vor dem x (ohne Vorzeichen) ist hier 3
Halbiert Quadriert Zuerst + danach - So erhalten wir:
Innerhalb der runden Klammer steht hier die zweite binomische Formel, da vor 3x ein Minus steht. (Hätte vor 3x ein Plus gestanden, hätte sich die erste binomische Formel ergeben.) |
| 4. Schritt:Binomische Formel umformen | 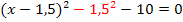
Ist dir dieser Schritt nicht klar, wiederhole bitte das Rechnen mit Binomischen Formeln! |
| 5. Schritt:Zusammenfassen so weit möglich | 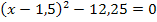
|
| 6. Schritt: Gleichung so umstellen, dass die Klammer mit dem Quadrat alleine steht, damit dann die Wurzel gezogen werden kann. Wurzel falls möglich ziehen und nach x auflösen!
Achtung: Plus/Minus vor der Wurzel nicht vergessen! |
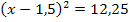 | | 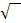
|
Nun folgt die zweite Variante der quadratischen Ergänzung zur Lösung gemischtquadratischer Gleichungen.

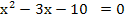
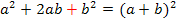
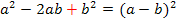
 1,5
1,5