Herleitung der Mitternachtsformel

Die Mitternachtsformel, also die Lösungsformel für gemischtquadratische Gleichungen, lautet bekanntlich:

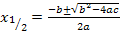
Sie wird verwendet zur Lösung von Gleichungen der Form 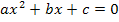mit 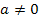. Mittels quadratischer Ergänzung wird die Mitternachtsformel hergeleitet.

Wir verwenden hier die erste oben gezeigte Methode der quadratischen Ergänzung. (Vergleiche 1. Variante!) So, nun Schritt für Schritt zur Mitternachtsformel.

Geg.: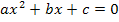   

1. Schritt:a ausklammern, d.h. jeden Faktor durch a teilen:

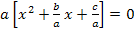
2. Schritt:Auf beiden Seiten der Gleichung durch a dividieren:

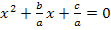
3. Schritt:Quadratisch ergänzen, um eine binomische Formel herzustellen, d.h. man nimmt den Term vor dem x (ohne Vorzeichen) halbiert und quadriert ihn;das addiert man zuerst und subtrahiert dann gleich wieder, damit sich an der Gleichung insgesamt nichts ändert.

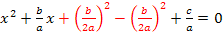
4. Schritt:Binomische Formel umformen

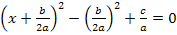
5. Schritt:Hinteren Teil zusammenfassen, also Klammer ausrechnen und Hauptnenner bilden

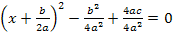
6. Schritt:  Gleichung so umstellen, dass die Klammer mit dem Quadrat alleine steht. Dann die rechte Seite der Gleichung auf einen Bruchstrich schreiben, die Wurzel ziehen und nach x auflösen:

|

|

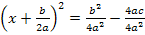
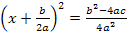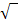
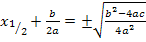
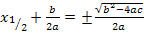
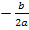
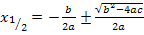
Nun schreiben wir alles auf der rechten Seite noch auf einen gemeinsamen Bruchstrich;beide Brüche haben bereits den gleichen Nenner, also brauchen wir nicht mehr erweitern. Somit erhalten wir die Mitternachtsformel.

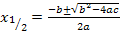
Wie du siehst, wird einfach nur die quadratische Ergänzung auf die allgemeine Form der gemischtquadratischen Gleichung angewendet, um die Mitternachtsformel herzuleiten. Es mag zwar durch die vielen vorkommenden Buchstaben etwas kompliziert erscheinen, doch eigentlich ist diese Herleitung eben nichts anderes als die quadratische Ergänzung angewendet auf den allgemeinen Fall einer gemischtquadratischen Gleichung. Du solltest jeden einzelnen Schritt nachvollziehen können. Selbst herleiten musst du die Formel aber auch in Prüfungen sicher nicht.