Graphische Lösungsverfahren quadratischer Gleichungen
Im folgenden Kapitel wird beschrieben, wie man mit Hilfe einer Zeichnung die Lösung(en) einer quadratischen Gleichung ermittelt. Es gibt dafür zwei etwas unterschiedliche Verfahren. Bei beiden Methoden verwendet man den Graph einer quadratischen Funktion, also eine Parabel. Deshalb ist es unerlässlich, dass du dich mit Parabeln schon auskennst. Du musst den Scheitel einer Parabel ermitteln und die Parabel in ein Koordinatensystem einzeichnen können. Wenn du das noch nicht (oder nicht mehr) kannst, bearbeite erst das Kapitel Quadratische Funktionen!
Nun sollen an Hand von Beispielen die beiden Methoden zur graphischen Lösung quadratischer Gleichungen vorgestellt und erläutert werden.
1. Methode:
Wir stellen die gegebene quadratische Gleichung so um, dass auf einer Seite der Gleichung nur noch Null steht, d.h. man bringt die Gleichung auf die Form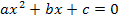 
. Hat die Gleichung bereits diese Form entfällt der erste Schritt natürlich.Nun stellen wir uns die linke Seite der Gleichung als quadratische Funktion f(x) = 
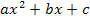vor. Du weißt, der Graph einer quadratischen Funktion ist immer eine Parabel. Wir können diese Parabel nur mit Hilfe ihres Scheitels und einer Parabelschablone, wenn es eine Normalparabel ist, oder sonst mit einer Wertetabelle in ein Koordinatensystem einzeichnen. Was hat aber nun diese Parabel mit unserer Gleichung zu tun?
Die x-Koordinaten der Nullstellen der Parabel f(x) =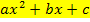 
, also ihre Schnittpunkte mit der x-Achse, sind die Lösungen der Gleichung 
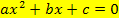! Wir müssen sie nur aus der Zeichnung so genau wie möglich ablesen. Jetzt frägst du dich wahrscheinlich:„Hä, warum denn das? Was haben denn nun die Nullstellen der Parabel mit den Lösungen unserer Gleichung zu tun?“ Das ist gar nicht so schwierig zu verstehen:Überlege dir ´mal, wie man die Nullstellen einer Funktion berechnet.
