Einführung in die quadratischen Gleichungen

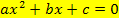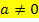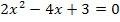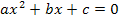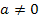Gleichungen vom Typ mit nennt man quadratische Gleichungen. Die Buchstaben a, b und c werden dabei als Koeffizienten bezeichnet. Die Gleichung ist beispielsweise eine quadratische Gleichung, da sie die oben erwähnte Form mit hat.

Es ist wichtig für dich, dass du es sofort erkennst, wenn eine quadratische Gleichung vorliegt, da solche Gleichungen nicht mehr so einfach nach x aufzulösen sind, wie zum Beispiel eine Gleichung, die kein 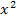enthält. Man muss dann nämlich ganz anders vorgehen. Wie man quadratische Gleichungen lösen kann, hängt vom Typ ab, also ob es sich z. B. um eine rein- oder gemischtquadratische Gleichung handelt. Daher müssen wir nachher auch diese Begriffe klären, bevor wir uns dann daran machen können, derartige Gleichungen zu lösen.

Das Entscheidende bei allen quadratischen Gleichungen ist auf jeden Fall, dass 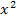in der Gleichung vorkommt. Etwas flappsig gesagt:Eine Gleichung, die ein 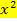(aber keine höhere Potenz von x) enthält, wird als quadratische Gleichung bezeichnet. Mathematisch geschrieben, also 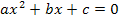mit .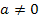

Warum aber darf a hier nicht gleich Null sein? Würde für a Null eingesetzt werden, würde eine Gleichung vom Typ 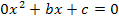entstehen, vereinfacht 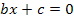also eine Gleichung ohne 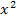! Dass so eine Gleichung nicht mehr quadratisch ist, dürfte klar sein:Es wäre ja gar kein 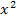mehr vorhanden! Es muss aber 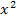in der Gleichung vorkommen, damit es sich um eine quadratische Gleichung handeln kann. 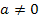ist also nichts anderes als die mathematisch korrekte Beschreibung, der Aussage, dass 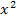bei einer quadratischen Gleichung nicht wegfallen darf. Die Koeffizienten b und c können allerdings schon gleich Null sein. D.h. das x (ohne Quadrat) oder die Zahl ohne x dürfen, eventuell sogar beide gleichzeitig, fehlen. So sind beispielsweise die Gleichungen 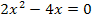und 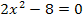beide quadratisch. Es sind nur Spezialfälle der allgemeinen quadratischen Gleichung 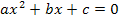mit .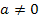

Vorsicht:Nicht jede Gleichung, die ein 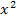enthält, ist auch wirklich quadratisch!

---