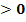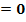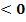Diskriminante D
Der Ausdruck unter der Wurzel der Mitternachtsformel 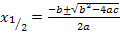 wird als Diskriminante D bezeichnet. (Lat. discriminare = unterscheiden, trennen)
wird als Diskriminante D bezeichnet. (Lat. discriminare = unterscheiden, trennen)
D 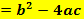
Vom Vorzeichen der Diskriminante hängt es ab, wie viele Lösungen eine gemischtquadratische Gleichung besitzt. Je nach Diskriminante hat sie zwei, genau eine oder gar keine Lösung. Der Zusammenhang von D mit der Anzahl der Lösungen wird klar, wenn man die Mitternachtsformel in der folgenden Form schreibt:
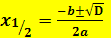 mitD
mitD 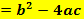
In dieser Form der Mitternachtsformel sieht man sofort, dass die Diskriminante D unter der Wurzel steht. Da man aus einer negativen Zahl keine Wurzel ziehen kann, hat die Gleichung 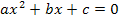 gar keine Lösung, wenn die Diskriminante negativ ist.
gar keine Lösung, wenn die Diskriminante negativ ist.
Ist die Diskriminante D positiv, lässt sich die Wurzel (zumindest näherungsweise) berechnen. Da man im Zähler der Mitternachtsformel einmal + 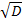 und einmal –
und einmal – 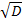 rechnen muss, ergeben sich bei positiver Diskriminante zwei verschiedene Lösungen für
rechnen muss, ergeben sich bei positiver Diskriminante zwei verschiedene Lösungen für 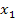 und
und 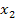 .
.
Ist die Diskriminante D gleich Null, erhält man für 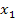 und
und 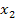 zweimal dieselbe Lösung, da sich das Gleiche ergibt, wenn man im Zähler der Mitternachtsformel einmal +
zweimal dieselbe Lösung, da sich das Gleiche ergibt, wenn man im Zähler der Mitternachtsformel einmal + 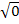 und einmal -
und einmal - 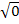 rechnet. (Bekanntlich ist +
rechnet. (Bekanntlich ist + 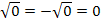 ) Daher gibt es nur eine einzige Lösung für x, wenn die Diskriminante gleich Null ist. Man bezeichnet diese Lösung als doppelte Lösung für x, da
) Daher gibt es nur eine einzige Lösung für x, wenn die Diskriminante gleich Null ist. Man bezeichnet diese Lösung als doppelte Lösung für x, da 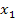
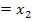 ist. Die beiden Lösungen fallen also zu einer einzigen (doppelten) Lösung zusammen.
ist. Die beiden Lösungen fallen also zu einer einzigen (doppelten) Lösung zusammen.
Wie viele Lösungen die Gleichung 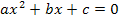 (mit
(mit 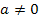 ) hat, kann somit ganz einfach mit Hilfe der Diskriminante D ermittelt werden.
) hat, kann somit ganz einfach mit Hilfe der Diskriminante D ermittelt werden.
Zusammenfassung: D 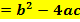 Diskriminante Diskriminante
Anzahl der Lösungen der Gleichung D
D
D |
Immer, wenn es in einer Aufgabe um die Anzahl der Lösungen geht, berechnet man zuerst nur die Diskriminante und verwendet nicht gleich die komplette Mitternachtsformel. Schauen wir uns ein paar Beispiele dazu an.
1. Bsp.:
Ermittle die Anzahl der Lösungen folgender Gleichungen, ohne die Lösungen explizit zu ermitteln!