Anwendungsaufgaben zu den quadratischen Gleichungen
In den verschiedensten Anwendungsaufgaben ergeben sich letztendlich rein- oder gemischtquadratische Gleichungen. Besonders im Gymnasium (G8) sind bei den Lehrern solche Aufgaben sehr beliebt – bei den Schülern wohl eher weniger. Weil man sich die Gleichung erst selbst mit Hilfe des Sachzusammenhangs aufstellen muss, beginnen da schon die Probleme der meisten Schüler. Es können auf dieser website natürlich nicht alle denkbaren Sachaufgaben, die zu quadratischen Gleichungen führen, vorgestellt werden. Im Folgenden findest du daher nur eine kleine Auswahl von typischen Anwendungs– und Sachaufgaben rund um das Thema quadratische Gleichungen.
1. Bsp.:
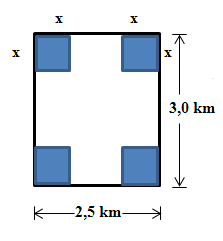
Skizze nicht maßstabsgetreu!
In die Ecken eines Rechtecks der Länge 3,0 km und der Breite 2,5 km sollen vier Quadrate (Siehe blaue Flächen in der Abbildung!) eingezeichnet werden, sodass die vier Quadrate zusammen genau 30 % der Rechtecksfläche einnehmen. Die Seitenlänge jeweils eines der Quadrate ist x km. ( 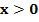 )
)
Hinweis zur Aufgabenstellung:
Meist werden heute die Aufgaben nicht mehr in diesem Stil gestellt. Stattdessen wirst du oft mit riesigen Texten konfrontiert, die aber letztendlich zur selben Rechnung führen. Die Aufgabenstellung zu dieser Aufgabe hätte beispielsweise auch folgendermaßen lauten können:
Wir haben ein großes rechteckiges, noch völlig unbebautes Grundstück der Länge 3,0 km und der Breite 2,5 km vorliegen, das nun teilweise bebaut werden soll. Der Bebauungsplan erlaubt jedoch nur eine Bebauung von 30% der Grundstückfläche. Es sollen jetzt vier Häuserblöcke mit identischer quadratischer Grundfläche auf diesem Grundstück errichtet werden. Vergleiche dazu den vorliegenden Bebauungsplan! (Die vier blau markierten Flächen entsprechen dabei den vier Häuserblöcken.) Wie breit darf einer dieser vier Häuserblöcke maximal sein, wenn die Vorgabe des Bebauungsplans eingehalten werden soll?
Bebauungsplan:
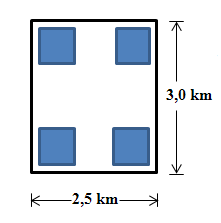
Du wunderst dich vielleicht darüber, dass der Bebauungsplan anders aussieht als die oben gezeigte Abbildung, obwohl es sich doch angeblich um die gleiche Rechnung handeln soll. Die Häuser werden nicht genau an den Ecken des Grundstücks plaziert, sondern etwas nach innen gerückt. Wenn du kurz darüber nachdenkst, wirst du feststellen, dass es für die bebaute Fläche gar keine Rolle spielt, wo innerhalb des Grundstücks die Häuser stehen. Deshalb ist das im Prinzip die gleiche Aufgabe, nur in einem Text verpackt.
So, nun willst du sicherlich endlich wissen, wie man denn die Aufgabe löst. Also, los geht´s!

