Quadratische Gleichungen

Du kannst nun auswählen, wofür du dich im Speziellen interessierst:

·        Was ist überhaupt eine quadratische Gleichung? Was ist der Unterschied zwischen rein- und gemischtquadratischen Gleichungen und warum ist diese Unterscheidung überhaupt wichtig? Was versteht man unter der normierten Form einer quadratischen Gleichung? Antworten auf diese Fragen findest du im Kapitel Einführung in die quadratischen Gleichungen. (Hier wird noch nicht gezeigt, wie man sie löst.)

·        Bevor quadratische Gleichungen auch rechnerisch gelöst werden sollen, sind vor allem in der 9. Klasse auf dem Gymnasium graphische Lösungen verlangt. Wie mit Hilfe einer Parabel, die Lösungen einer quadratischen Gleichung ermittelt werden können, wird erklärt im Kapitel Graphische Lösungsverfahren quadratischer Gleichungen.

·Für alle Schüler ab der 9. Klasse extrem wichtig:

Rechnerische Lösungsverfahren quadratischer Gleichungen

·        Wie löst man rein- bzw. gemischtquadratische Gleichungen rechnerisch? Was ist Die Mitternachtsformel?

·        Wie ermittelt man die Anzahl der Lösungen einer gemischtquadratischen Gleichung und was versteht man unter der Diskriminante D?

·        Was ist eine Substitution? Wie löst man biquadratische Gleichungen, also Gleichungen der Form ?

·        Wie lassen sich gemischtquadratische Gleichungen mit Hilfe der quadratischen Ergänzung lösen? Das findest du bei Quadratische Ergänzung (zur Lösung gemischtquadratischer Gleichungen)

·        Wie geht die Herleitung der Mitternachtsformel mittels quadratischer Ergänzung?

Das wird alles mit vielen Beispielen genau erklärt in diesem Kapitel.

·        Wie man im Kopf manchmal relativ schnell die Lösungen einer gemischtquadratischen Gleichung finden kann, wird gezeigt im Kapitel Satz von Vieta.

·        Besonders für Gymnasiasten der 9. Klasse (G8) sind die verschiedensten Anwendungsaufgaben (Textaufgaben), die letztendlich zu einer quadratischen Gleichung führen, extrem wichtig. Ausgewählte Beispiele findest du bei den Anwendungsaufgaben zu den quadratischen Gleichungen
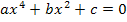