Wertemenge und Symmetrieachse

Wertemenge einer quadratischen Funktion ermitteln:

Die Wertemenge 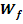bezieht sich immer auf die y-Werte. Sie enthält genau die y-Werte, die bei der Funktion 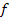, also hier bei der Parabel, herauskommen können. In anderen Worten:Die Wertemenge enthält alle Werte, welche die Funktion 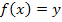annehmen kann. Denk´daran, dass 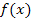nur eine andere Schreibweise für y darstellt. Es geht also darum, wie hoch der Graph im Koordinatensystem liegt.

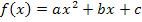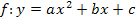In manchen Aufgaben soll die Wertemenge einer quadratischen Funktion bzw. angeben werden. Im Prinzip muss dazu nur der Scheitelpunkt S der Parabel, genauer gesagt sogar nur die y-Koordinate 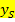des Scheitels, ermittelt werden. Wie das geht, wird im Kapitel Berechnung des Scheitelpunktsausführlich erklärt. Liegt die Parabel bereits in Scheitelform 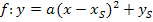vor, kann 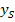direkt abgelesen werden. Sobald 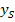bekannt ist, ist es ganz einfach die Wertemenge 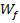der Funktion anzugeben. Man muss sich jetzt nur noch überlegen, ob die Parabel nach oben oder nach unten geöffnet ist. Das hängt ausschließlich vom Vorzeichen des Öffnungsfaktors a ab, d.h. von der Zahl, die in der allgemeinen Form der Parabel vor bzw. in der Scheitelform vor der Klammer steht.

Ist a positiv, ist die Parabel nach oben geöffnet und der Scheitel ist das absolute Minimum der Parabel. Der Scheitel ist für 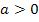der Punkt des Graphen 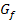, der am tiefsten liegt. Die y-Koordinate des Scheitels ist dann der kleinste Wert, den die Funktion annehmen kann;alle anderen y-Werte von 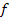sind größer.

---