Symmetrieachse und zwei weitere Informationen gegeben
In manchen Aufgaben ist unter anderem die Symmetrieachse der Parabel gegeben. Soll die Gleichung einer Parabel aufgestellt werden, ist diese Information als Angabe der x-Koordinate des Scheitels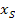 
zu sehen. Die Gleichung der Symmetrieachse einer Parabel mit dem Scheitelpunkt 
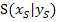lautet: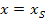 
Daher ist die Angabe der Symmetrieachse nichts anderes als die Angabe der x-Koordinate des Scheitels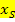 
.
Ist dir das noch nicht wirklich klar, stellst du dir am besten einfach eine beliebige Parabel vor, beispielweise die Parabel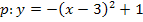 
. Der Scheitel S(3|1) der Parabel kann sofort abgelesen werden, da die Parabel bereits in der Scheitelform 
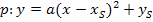vorliegt. Überlege dir, wo du ihre Symmetrieachse einzeichnen würdest. Du wirst feststellen, dass die Symmetrieachse genau durch den Scheitel und senkrecht zur x-Achse verläuft. Die Symmetrieachse einer quadratischen Funktion, also einer nach oben oder unten geöffneten Parabel, ist immer eine senkrechte Gerade.
Bekanntlich haben senkrechte Geraden – sie sind übrigens keine Funktionen – die Gleichung x = Zahl. (Genauere Erläuterungen zu senkrechten Geraden findest du im Kapitel Waagrechte und senkrechte Geraden) In unserem Beispiel verläuft die Symmetrieachse im Abstand 3 parallel zur y-Achse. Siehe Abb.! Sie muss daher die Gleichung x = 3 haben. (Anmerkung:Alle Punkte, die auf dieser Gerade liegen, haben zwar verschiedene y-Koordinaten, aber sie haben alle die x-Koordinate x = 3. Daher kommt die Gleichung der Symmetrieachse in diesem Beispiel.) Vergleicht man dies mit der x-Koordinate des Scheitels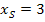 
, stellt man fest, dass die Symmetrieachse mit der x-Koordinate des Scheitels 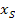übereinstimmt.
