Scheitel und ein weiterer Kurvenpunkt gegeben
Ist der Scheitelpunkt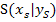 
und ein Kurvenpunkt A gegeben, ist es nicht besonders schwer die Parabelgleichung aufzustellen. Da der Scheitel bekannt ist, verwendet man natürlich die Scheitelform als allgemeinen Ansatz.
Man braucht dann nur die Scheitelkoordinaten für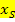 
bzw. 
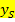und die Koordinaten des Kurvenpunktes für x bzw. y in die Scheitelform 
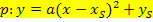einsetzen, um eine Gleichung, die nur a als Unbekannte enthält, zu erhalten. Durch Auflösen dieser Gleichung nach a kann der Koeffizient a leicht berechnet werden.
Dann setzt man den soeben ermittelten Wert für a und die Scheitelkoordinaten für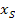 
bzw.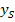 
in die Scheitelform 
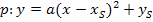ein. Danach wird in die allgemeine Form umgerechnet, indem man mit Hilfe der ersten oder zweiten binomischen Formel die Klammer quadriert, dann a in die Klammer hinein multipliziert und soweit möglich zusammenfasst. Danach liegt die Parabel in ihrer allgemeinen Form 
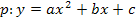vor.
Hinweis:Die meisten Schüler haben zwar kein Problem a zu berechnen, doch sie wissen oftmals nicht, wie es dann weiter geht, d.h. wo sie den gerade berechneten Wert von a dann einsetzen sollen. Solltest du dieses Problem ebenfalls haben, hilft oft folgendes Vorgehen:
Setze zu Beginn deiner Rechnung vorerst nur den Scheitelpunkt in die Scheitelform ein! Erst dann setzt du in einem zweiten Schritt zusätzlich auch die Koordinaten des Kurvenpunkts A in diese Gleichung ein. Nun kannst du a leicht berechnen. Das Ergebnis setzt du danach für a in deine als erstes aufgestellte Gleichung ein, also in die Scheitelform, wo du nur die Scheitelkoordinaten, aber eben nicht den Kurvenpunkt eingesetzt hast.
