Öffnungsfaktor a und Scheitelpunkt S gegeben
Ist der Koeffizient a (also die Zahl, die in der allgemeinen Form einer Parabel vor 
bzw. in der Scheitelform vor der Klammer steht) und der Scheitelpunkt 
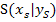gegeben, braucht man nur a und die Scheitelkoordinaten in die Scheitelform 
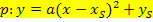einsetzen, um die Parabelgleichung aufzustellen. Danach wird in die allgemeine Form umgerechnet, indem man mit Hilfe der ersten oder zweiten binomischen Formel die Klammer quadriert, dann a in die Klammer hinein multipliziert und soweit möglich zusammenfasst. Danach liegt die Parabel in ihrer allgemeinen Form 
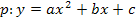vor.
1. Bsp.:Eine Parabel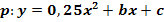 
hat den Scheitelpunkt S(1|-4). Ermittle die Koeffizienten b und c!
Lösung:
Laut Angabe ist a = 0,25 und der Scheitel hat die Koordinaten S(1|-4), d.h. die x-Koordinate des Scheitels ist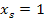 
und die y-Koordinate des Scheitels ist 
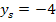. Da der Scheitel bekannt ist, verwendet man die Scheitelform und setzt die angegebene Werte für a, 
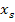und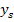 
ein. Vorsicht:Die Scheitelkoordinaten werden für 
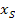und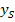 
eingesetzt und nicht für x und y! Für x und y darf gar nichts eingesetzt werden, wenn man die Scheitelform aufstellen will!
Scheitelform (allgemeiner Ansatz):
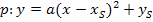
a, 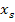und 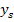einsetzen: 
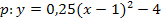(Scheitelform von p)
2. Binomische Formelanwenden: 
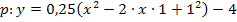
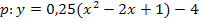
a in die Klammer hinein multiplizieren: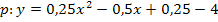 
Zusammenfassen: 
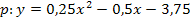
Die Parabelgleichung ist nun in der Form 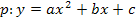aufgestellt. Der Koeffizient b ist die Zahl vor x (einschließlich des Vorzeichens), der Koeffizient c ist die Zahl ohne x (ebenfalls einschließlich des Vorzeichens).
Die gesuchten Koeffizienten können jetzt einfach abgelesen werden:b = -0,5 und c = -3,75
2. Bsp.:
Durch Verschiebung der Parabel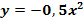 
um 4 nach links und 7 nach oben entsteht die Parabel p. Ermittle die Gleichung der Parabel p in der Form 
!
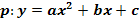Lösung:
Die Parabel p entsteht durch eine Verschiebung der Parabel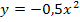 
, daher ändert sich nichts am Öffnungsfaktor a, also an der Zahl vor . Deshalb muss auch die gesuchte Parabel p den Öffnungsfaktor a = -0,5 haben. Es müssen also nur noch die Koeffizienten b und c ermittelt werden.
Die Parabel 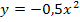hat ihren Scheitel im Ursprung (0|0). Da diese Parabel um 4 nach links und 7 nach oben verschoben wird, muss der Scheitel der gesuchten Parabel bei S(-4|7) liegen.
Anmerkung:Man hätte diese Aufgabe auch deutlich einfacher formulieren können. Ermittle die Gleichung einer Parabel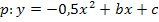 
mit dem Scheitel S(-4|7)! Das ist im Prinzip die gleiche Aufgabe, eben nur einfacher gestellt. Da es leider nicht immer so deutlich gefragt wird, wurde hier absichtlich einmal die schwierigere Fragestellung vorgeführt.
Gegeben sind also a = -0,5 und der Scheitelpunkt S(-4|7). Man braucht deshalb nur in die Scheitelform einsetzen und danach in die Form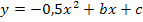 
umrechnen.
Scheitelform (allgemeiner Ansatz):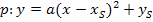
a = -0,5 und S(-4|7) einsetzen: 
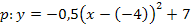
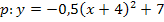(Scheitelform von p)
1. Binomische Formelanwenden: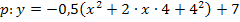 
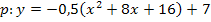
Ausmultiplizieren: 
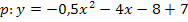
Zusammenfassen: 
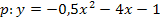
Nun ist die Gleichung der Parabel p in der gesuchten Form ermittelt.
| Zusammenfassung:
Gesucht: Gleichung einer Parabel mit Scheitel · Scheitelform als allgemeiner Ansatz · a und die Scheitelkoordinaten für · Scheitelform umrechnen in die allgemeine Form |
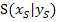mit bekannten Öffnungsfaktor a
Scheitelform
