Normalparabel (nach oben oder unten geöffnet) und zwei Kurvenpunkte gegeben
Soll laut Angabe die Funktionsgleichung einer nach oben geöffneten Normalparabel p ermittelt werden, weißman sofort, dass der Koeffizient a = 1 sein muss, dass also vor 
keine Zahl in der Funktionsgleichung steht.
Allgemeiner Ansatz für eine nach oben geöffnete Normalparabel: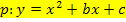 
Soll laut Angabe die Funktionsgleichung einer nach unten geöffneten Normalparabel p ermittelt werden, weißman sofort, dass der Koeffizient a = -1 sein muss, dass also vor nur ein Minuszeichen in der Funktionsgleichung steht.
Allgemeiner Ansatz für eine nach unten geöffnete Normalparabel: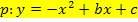 
Durch die Angabe „nach oben bzw. nach unten geöffnete Normalparabel“ ist der Koeffizient a also praktisch direkt gegeben.
Es müssen daher nur noch die beiden Koeffizienten b und c berechnet werden. Um zwei Unbekannte berechnen zu können, braucht man zwei Gleichungen.
Zur Erinnerung:Man benötigt immer genauso viele Gleichungen, wie man Unbekannte hat, die man berechnen soll.
Die beiden benötigten Gleichungen erhält man, in dem man die Koordinaten der beiden Kurvenpunkte für x bzw. y in den allgemeinen Ansatz einsetzt. Man setzt also zuerst die x- und y-Koordinate des einen gegebenen Kurvenpunktes in den allgemeinen Ansatz der nach oben geöffnete Normalparabel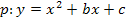 
bzw. in den allgemeinen Ansatz der nach unten geöffneten Normalparabel 
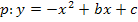für x bzw. y ein;das ergibt die erste Gleichung. Wir bezeichnen sie mit I. Danach verfährt man mit dem zweiten gegeben Punkt entsprechend. Dadurch erhält man die zweite benötigte Gleichung II. Die beiden Gleichungen I und II werden am besten direkt untereinander geschrieben.
