Normalparabel (nach oben oder unten geöffnet) und Scheitelpunkt S gegeben
Da der Scheitelpunkt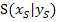 
gegeben ist, verwendet man die Scheitelform einer Parabelals allgemeinen Ansatz für die Parabel p.
Scheitelform einer Parabel: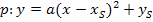 
Soll laut Angabe die Funktionsgleichung einer nach oben geöffneten Normalparabel p ermittelt werden, weißman, dass der Koeffizient a = 1 sein muss, dass also vor der Klammer in der Scheitelform keine Zahl steht.
Allgemeiner Ansatz (Scheitelform) für eine nach oben geöffnete Normalparabel:
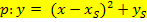
Soll laut Angabe die Funktionsgleichung einer nach unten geöffneten Normalparabel p ermittelt werden, weißman sofort, dass der Koeffizient a = -1 sein muss, dass also vor der Klammer in der Scheitelform nur ein Minus-Zeichen steht.
Allgemeiner Ansatz (Scheitelform) für eine nach unten geöffnete Normalparabel:
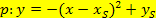
Durch die Angabe „nach oben bzw. nach unten geöffnete Normalparabel“ ist der Koeffizient a also im Prinzip direkt gegeben.
Da der Scheitelpunkt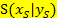 
gegeben ist, braucht man ihn nur in die Scheitelform (allgemeiner Ansatz) einsetzen und dann soweit möglich vereinfachen. Mit Vereinfachen ist gemeint, mit Hilfe der ersten oder zweiten binomischen Formel die Klammer zu quadrieren, dann zumindest bei nach unten geöffneten Parabeln das Minus-Zeichen, d.h. -1, in die Klammer hinein zu multiplizieren und dann noch die beiden hinteren Zahlen zusammen zu rechnen. So entsteht die gesuchte allgemeine Form (a,b,c-Form) der Parabel.
Du solltest die Scheitelform immer in die allgemeine Form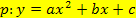 
umrechnen;das ist in der Regel nämlich verlangt, obwohl es nicht immer in der Aufgabenstellung explizit erwähnt ist.
