Ein Koeffizient (a, b oder c) und zwei Kurvenpunkte gegeben
Ist von einer Parabel p einer der Koeffizienten a, b oder c gegeben und sind außerdem noch zwei Kurvenpunkte A und B bekannt, geht man von der Normalform aus.
Allgemeiner Ansatz für eine Parabel:![]()
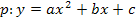
Zuerst wird der bekannte Koeffizient eingesetzt. Nun müssen die anderen beiden Koeffizienten berechnet werden. Um zwei Unbekannte berechnen zu können, benötigt man zwei Gleichungen I und II, ein sogenanntes Gleichungssystem. Man erhält diese Gleichungen, indem man für x bzw. y jeweils die Koordinaten des ersten und danach die des zweiten Kurvenpunktes einsetzt. Jetzt wird entweder mit Hilfe des Additions- oder des Einsetzungsverfahrens das Gleichungssystem gelöst. Dadurch erhält man die beiden gesuchten Koeffizienten. Diese werden noch in den allgemeinen Ansatz der Parabel eingesetzt;dann ist die Gleichung der Parabel aufgestellt.
Kurzwiederholung des Einsetzungsverfahrens:
Eine der beiden Gleichungen (z.B. I) wird nach einer der beiden Unbekannten aufgelöst und in die andere Gleichung (hier II) eingesetzt. Dadurch erhält man eine Gleichung, die nur noch eine Unbekannte enthält. Nun kann diese verbliebene Unbekannte durch Umstellen dieser Gleichung berechnet werden. Ist die eine Unbekannte bekannt, setzt man sie in eine der beiden Gleichungen I oder II ein. Ebenfalls durch Umstellen kann nun die zweite Unbekannte ermittelt werden.
Kurzwiederholung des Additionsverfahrens:
Die beiden Gleichungen I und II werden falls nötig so mit Faktoren (Zahlen) multipliziert, dass sich vor einer der beiden Unbekannten in beiden Gleichungen, vom Vorzeichen einmal abgesehen, die gleichen Zahlen ergeben. Die beiden so gebildeten Gleichungen werden nun addiert bzw. subtrahiert, so dass dabei eine der beiden Unbekannten wegfällt. Es entsteht dadurch eine Gleichung, die nur noch eine Unbekannte enthält. Die verbliebene Unbekannte lässt sich jetzt leicht durch Umstellen dieser Gleichung berechnen. Nun ist eine Unbekannte ermittelt;sie wird in eine der ursprünglichen Gleichungen I oder II eingesetzt. Dadurch kann jetzt auch die zweite Unbekannte nur durch Umstellen der entstandenen Gleichung ermittelt werden.

