Drei Kurvenpunkte gegeben
(Nicht für Realschüler!)
Drei Punkte, welche auf der Parabel p liegen, sind gegeben. Damit soll die Gleichung einer Parabel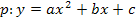 
ermittelt werden. Man muss also die Koeffizienten a, b und c bestimmen. Dazu setzt man der Reihe nach die Koordinaten der Kurvenpunkte für x bzw. y in den allgemeinen Ansatz 
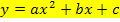ein. (Die Scheitelform der Parabel als allgemeinen Ansatz zu verwenden, würde natürlich keinen Sinn machen, da der Scheitel nicht bekannt ist.) Man setzt also zuerst die Koordinaten des ersten angegeben Kurvenpunktes in den allgemeinen Ansatz y = 
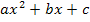für x und y ein. Es entsteht eine Gleichung mit den Unbekannten a, b und c;wir nennen sie Gleichung I. Dann setzt man die Koordinaten des zweiten Kurvenpunkts in 
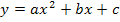für x und y ein. Das ergibt die Gleichung II. Entsprechend verfährt man mit dem dritten Kurvenpunkt. Das führt zu Gleichung III. So entsteht ein Gleichungssystem mit drei Gleichungen und den drei Unbekannten a, b und c.
Mit drei Kurvenpunkten die Gleichung einer Parabel aufzustellen, dauert in der Regel ziemlich lange, weil es meist sehr aufwendig ist, dieses Gleichungssystem mit seinen drei Gleichungen und drei Unbekannten zu lösen. Ein wesentlich einfacherer Sonderfall liegt allerdings vor, wenn einer der bekannten Kurvenpunkte die x-Koordinate x = 0 besitzt. Dann ergibt sich nämlich der Koeffizient c direkt, wenn man diesen Kurvenpunkt in den allgemeinen Ansatz 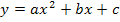einsetzt. (Vergleiche dazu 1. Bsp. weiter unten!
