Beide Nullstellen und ein weiterer Kurvenpunkt oder ein Koeffizient a, b oder c gegeben

1. Beide Nullstellen und ein weiterer Kurvenpunkt bekannt:

Sind beide Nullstellen einer Parabel sowie ein anderer Kurvenpunkt gegeben, empfiehlt es sich von der faktorisierten Form (= Produktform) der quadratischen Funktion, also der Parabel, auszugehen, um die Parabelgleichung aufzustellen.

Faktorisierte Form einer Parabel p mit den Nullstellen 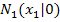und :

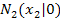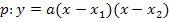(Allgemeiner Ansatz)

Man setzt nun für 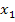bzw. 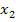die x-Koordinaten der beiden Nullstellen und für x bzw. y die Koordinaten des weiteren Kurvenpunktes ein. So entsteht eine Gleichung, die nur noch a als einzige Unbekannte enthält. Diese Gleichung wird dann nach a aufgelöst. Nun ist der Öffnungsfaktor a bereits ermittelt. Setzt man den soeben berechneten Wert für a und die x-Koordinaten der beiden Nullstellen für 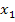bzw. 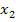wieder in den allgemeinen Ansatz der faktorisierten Form einer Parabel ein, erhält man die Gleichung der gesuchten Parabel p in faktorisierter Form. Soll die Parabel in der Form 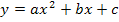aufgestellt werden, muss man nur noch ausmultiplizieren und soweit möglich zusammenfassen. Dann liegt die Parabel in der gewünschten Form vor.

Hinweis:Die meisten Schüler haben kein Problem a zu ermitteln, wenn sie überhaupt auf die Idee gekommen sind mit der faktorisierten Form zu arbeiten. Oft tritt dann jedoch das Problem auf, dass sie nicht wissen, wie es danach weiter geht. Solltest du vor dem gleichen Problem stehen, empfiehlt es sich folgendermaßen vorzugehen:

Setze zuerst nur die beiden x-Koordinaten der beiden Nullstellen für 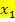bzw. 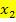in den allgemeinen Ansatz der faktorisierten Form der Parabel ein. Erst in einem zweiten Schritt setzt du dann auch die Koordinaten des anderen Kurvenpunktes für x und y ein. Nun berechnest du a und setzt das Ergebnis wieder in die oberste Gleichung für a ein, also in die Gleichung, in der du nur die x-Koordinaten der Nullstellen eingesetzt hast, aber noch nicht den Kurvenpunkt.

---